题目内容
已知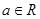 ,函数
,函数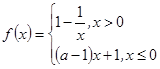 .
.
(I)证明:函数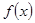 在
在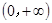 上单调递增;
上单调递增;
(Ⅱ)求函数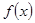 的零点.
的零点.
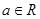 ,函数
,函数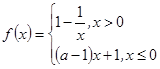 .
.(I)证明:函数
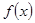 在
在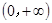 上单调递增;
上单调递增;(Ⅱ)求函数
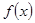 的零点.
的零点.(I)详见解析;(Ⅱ)详见解析;
试题分析:(I)先在
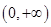 上任取两变量
上任取两变量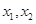 ,设
,设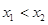 ,再对
,再对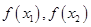 作差变形化简,判断
作差变形化简,判断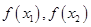 大小确定单调性.
大小确定单调性.(Ⅱ)要求函数f(x)的零点,即求方程f(x)=0的根,对
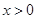 和
和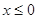 分情况求解,其中当
分情况求解,其中当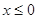 时,令
时,令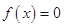 , 即
, 即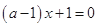 ,对此方程中参数a对根的情况进行讨论求解.
,对此方程中参数a对根的情况进行讨论求解.试题解析: (1)证明:在
 上任取两个实数
上任取两个实数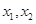 ,且
,且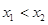 ,
,则
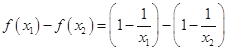
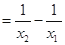
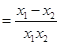 . 2分
. 2分∵
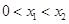 , ∴
, ∴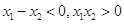 .
.∴
 , 即
, 即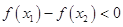 . ∴
. ∴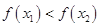 .
.∴函数
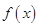 在
在 上单调递增. 4分[K]
上单调递增. 4分[K](2) (ⅰ)当
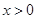 时, 令
时, 令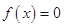 , 即
, 即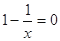 , 解得
, 解得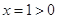 .
.∴
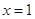 是函数
是函数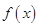 的一个零点. 6分
的一个零点. 6分(ⅱ)当
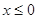 时, 令
时, 令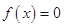 , 即
, 即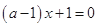 .(※)
.(※)①当
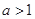 时, 由(※)得
时, 由(※)得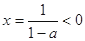 ,∴
,∴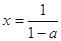 是函数
是函数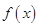 的一个零点; 8分
的一个零点; 8分②当
 时, 方程(※)无解;
时, 方程(※)无解;③当
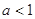 时, 由(※)得
时, 由(※)得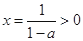 ,(不合题意,舍去) 10分
,(不合题意,舍去) 10分综上, 当
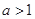 时, 函数
时, 函数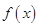 的零点是
的零点是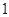 和
和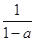 ;
; 当
 时, 函数
时, 函数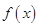 的零点是
的零点是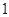 . 12分
. 12分
练习册系列答案
相关题目
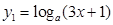 ,
, ,其中
,其中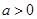 且
且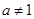 .
.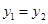 ,求
,求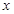 的值; (II) 若
的值; (II) 若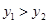 ,求
,求 内有一动点
内有一动点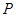 ,
,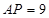 ,作
,作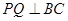 于
于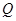 ,
,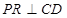 于
于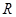 ,求矩形
,求矩形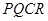 面积的最小值和最大值,并指出取最大值时
面积的最小值和最大值,并指出取最大值时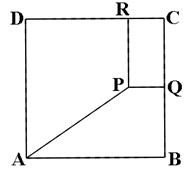
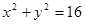 的周长和面积同时分为相等的两部分的函数称为圆
的周长和面积同时分为相等的两部分的函数称为圆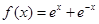
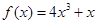
 在
在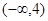 上是增函数,则实数
上是增函数,则实数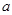 的范围是( )
的范围是( )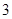
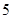
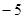
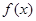 在区间
在区间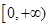 单调递减,则满足
单调递减,则满足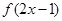
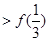 的
的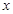 取值范围是( )
取值范围是( )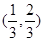
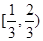
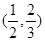

 .若
.若 ,则
,则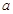 的取值范围是
的取值范围是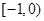
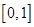
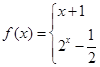
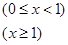 ,设
,设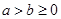 ,若
,若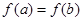 ,则
,则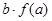 的取值范围是 ___ .
的取值范围是 ___ .