题目内容
2.已知数列{an}满足a1=2,an+1=an2,则数列{an}的通项公式为 an=${2}^{{2}^{n-1}}$.分析 an+1=an2,可得lgan+1=2lgan,再利用等比数列的通项公式即可得出.
解答 解:∵an+1=an2,
∴lgan+1=2lgan,
∴数列{lgan}是等比数列,首项lg2,公比为2.
∴lgan=2n-1lg2,
∴an=${2}^{{2}^{n-1}}$.
故答案为:${2}^{{2}^{n-1}}$.
点评 本题考查了等比数列的通项公式、对数的运算性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
17.已知函数f(x)=x3+bx2+cx+d的图象如图所示,则函数y=log${\;}_{\frac{1}{2}}$(x2+$\frac{2}{3}$bx+$\frac{c}{3}$)的单调减区间为( )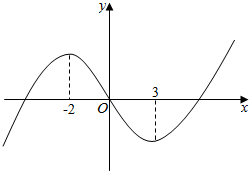

| A. | ($\frac{1}{2}$,+∞) | B. | (3,+∞) | C. | (-∞,-$\frac{1}{2}$) | D. | (-∞,-2) |