题目内容
已知函数f(x)=loga 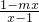 (a>0,且a≠1)在其定义域上是奇函数,则m=
(a>0,且a≠1)在其定义域上是奇函数,则m=
- A.1-

- B.-1
- C.-

- D.-

B
分析:利用奇函数的定义,结合对数的运算性质,即可求得结论.
解答:∵函数f(x)=loga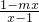 (a>0,且a≠1)在其定义域上是奇函数,
(a>0,且a≠1)在其定义域上是奇函数,
∴f(-x)+f(x)=0,即loga +loga
+loga 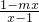 =0
=0
∴ ×
×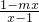 =1
=1
∴1-m2x2=1-x2
∴m2=1
∴m=±1
当m=1时, ,不合题意;当m=-1时,f(x)=loga
,不合题意;当m=-1时,f(x)=loga 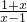 ,符合题意
,符合题意
故选B.
点评:本题考查函数的奇偶性,考查对数的运算性质,属于基础题.
分析:利用奇函数的定义,结合对数的运算性质,即可求得结论.
解答:∵函数f(x)=loga
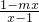 (a>0,且a≠1)在其定义域上是奇函数,
(a>0,且a≠1)在其定义域上是奇函数,∴f(-x)+f(x)=0,即loga
 +loga
+loga 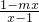 =0
=0∴
 ×
×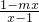 =1
=1∴1-m2x2=1-x2
∴m2=1
∴m=±1
当m=1时,
 ,不合题意;当m=-1时,f(x)=loga
,不合题意;当m=-1时,f(x)=loga 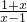 ,符合题意
,符合题意故选B.
点评:本题考查函数的奇偶性,考查对数的运算性质,属于基础题.

练习册系列答案
相关题目