题目内容
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)在x=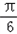 取得最大值2,方程f(x)=0的两个根为x1、x2,且|x1﹣x2|的最小值为π.
取得最大值2,方程f(x)=0的两个根为x1、x2,且|x1﹣x2|的最小值为π.
(1)求f(x);
(2)将函数y=f(x)图象上各点的横坐标压缩到原来的 ,纵坐标不变,得到函数y=g(x)的图象,求函数g(x)在[﹣
,纵坐标不变,得到函数y=g(x)的图象,求函数g(x)在[﹣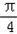 ,
,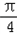 ]上的值域.
]上的值域.
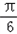 取得最大值2,方程f(x)=0的两个根为x1、x2,且|x1﹣x2|的最小值为π.
取得最大值2,方程f(x)=0的两个根为x1、x2,且|x1﹣x2|的最小值为π. (1)求f(x);
(2)将函数y=f(x)图象上各点的横坐标压缩到原来的
 ,纵坐标不变,得到函数y=g(x)的图象,求函数g(x)在[﹣
,纵坐标不变,得到函数y=g(x)的图象,求函数g(x)在[﹣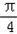 ,
,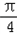 ]上的值域.
]上的值域.解:(1)由题意A=2,函数f(x)最小正周期为2 π,即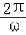 =2π,
=2π,
∴ω=1.从而f(x)=2sin(x+φ),
∵f(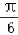 )=2,
)=2,
∴sin(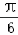 +φ)=1,
+φ)=1,
则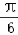 +φ=
+φ=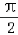 +2kπ,即φ=
+2kπ,即φ= 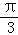 +2kπ,k∈z
+2kπ,k∈z
∵0<φ<π,
∴φ=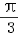 .
.
故f(x)=2sin(x+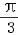 ).
).
(2)函数y=f(x)图象上各点的横坐标压缩到原来的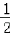 ,纵坐标不变,得到函数y=g(x)=f(2x)的图象,即g(x)=2sin(2x+
,纵坐标不变,得到函数y=g(x)=f(2x)的图象,即g(x)=2sin(2x+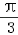 ),
),
当x∈[﹣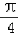 ,
,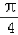 ]时,2x+
]时,2x+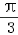 ∈[﹣
∈[﹣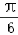 ,
,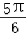 ],
],
则sin(2x+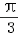 )∈[﹣
)∈[﹣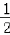 ,1],
,1],
故函数g(x)的值域是[﹣1,2].
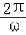 =2π,
=2π,∴ω=1.从而f(x)=2sin(x+φ),
∵f(
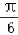 )=2,
)=2,∴sin(
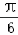 +φ)=1,
+φ)=1,则
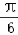 +φ=
+φ=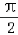 +2kπ,即φ=
+2kπ,即φ= 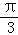 +2kπ,k∈z
+2kπ,k∈z ∵0<φ<π,
∴φ=
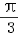 .
.故f(x)=2sin(x+
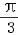 ).
).(2)函数y=f(x)图象上各点的横坐标压缩到原来的
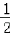 ,纵坐标不变,得到函数y=g(x)=f(2x)的图象,即g(x)=2sin(2x+
,纵坐标不变,得到函数y=g(x)=f(2x)的图象,即g(x)=2sin(2x+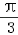 ),
),当x∈[﹣
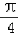 ,
,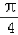 ]时,2x+
]时,2x+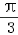 ∈[﹣
∈[﹣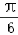 ,
,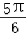 ],
],则sin(2x+
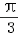 )∈[﹣
)∈[﹣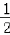 ,1],
,1],故函数g(x)的值域是[﹣1,2].

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目