题目内容
【题目】已知函数f(x)的定义域为R,且f(2)=2,又函数f(x)的导函数y=f′(x)的图象如图所示,若两个正数a、b满足f(2a+b)<2,则 ![]() 的取值范围是( )
的取值范围是( ) 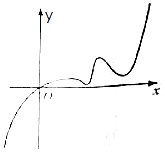
A.( ![]() ,2)
,2)
B.(﹣∞, ![]() )∪(2,+∞)
)∪(2,+∞)
C.(2,+∞)
D.(﹣∞, ![]() )
)
【答案】A
【解析】解:由图可知,当x>0时,导函数f'(x)>0,原函数单调递增, ∵两正数a,b满足f(2a+b)<2,
又由f(2)=2,即f(2a+b)<2,
即2a+b<2,
又由a>0.b>0;
故a,b所对应的平面区域如下图所示: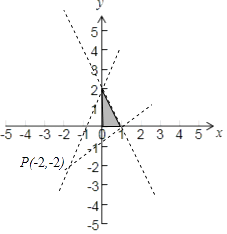
![]() 表示动点(a,b)与定点(﹣2,﹣2)连线的斜率,
表示动点(a,b)与定点(﹣2,﹣2)连线的斜率,
当直线过(1,0)点时, ![]() =
= ![]() ,
,
当直线过(0,2)点时, ![]() =2,
=2,
故 ![]() ∈(
∈( ![]() ,2),
,2),
故选:A.
【考点精析】本题主要考查了利用导数研究函数的单调性的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减才能正确解答此题.
在这个区间单调递减才能正确解答此题.

练习册系列答案
相关题目
【题目】某市要对该市六年级学生进行体育素质调查测试,现让学生从“跳绳、短跑![]() 米、长跑
米、长跑![]() 米、仰卧起坐、游泳
米、仰卧起坐、游泳![]() 米、立定跳远”
米、立定跳远”![]() 项中选择
项中选择![]() 项进行测试,其中“短跑、长跑、仰卧起坐”
项进行测试,其中“短跑、长跑、仰卧起坐”![]() 项中至少选择其中
项中至少选择其中![]() 项进行测试.现从该市六年级学生中随机抽取了
项进行测试.现从该市六年级学生中随机抽取了![]() 名学生进行调查,他们选择的项目中包含“短跑、长跑、仰卧起坐”的项目个数及人数统计如下表:(其中
名学生进行调查,他们选择的项目中包含“短跑、长跑、仰卧起坐”的项目个数及人数统计如下表:(其中![]() )
)
选择的项目中包含“短跑、长跑、仰卧起坐”的项目个数 |
|
|
|
人数 |
|
|
|
已知从所调查的![]() 名学生中任选
名学生中任选![]() 名,他们选择“短跑、长跑、仰卧起坐”的项目个数不相等概率为
名,他们选择“短跑、长跑、仰卧起坐”的项目个数不相等概率为![]() ,记
,记![]() 为这
为这![]() 名学生选择“短跑、长跑、仰卧起坐”的项目个数之和.
名学生选择“短跑、长跑、仰卧起坐”的项目个数之和.
(1)求![]() 的值;
的值;
(2)求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.