题目内容
椭圆 的焦点为F1和F2,过点F1的直线l交椭圆于P,Q两点,且
的焦点为F1和F2,过点F1的直线l交椭圆于P,Q两点,且 ,
,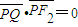 ,则椭圆的离心率为( )
,则椭圆的离心率为( )A.

B.

C.
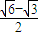
D.

【答案】分析:利用椭圆的定义可求得直角三角形PQF2的周长,进一步可求得|PF2|与|PF1|,在直角三角形PF1F2中可求得|F1F2|,从而可求得答案.
解答:解:由椭圆的定义得:|PF1|+|PF2|=2a,|QF1|+|QF2|=2a,

∴△PQF2的周长为l=4a;
∵ ,
, ,
,
∴△PQF2为等腰直角三角形,设|PF2|=x,
则x+x+ x=4a,
x=4a,
∴x= =
= a,
a,
∵|PF1|+|PF2|=2a,
∴|PF1|=2a-|PF2|=2a- a=
a= a,
a,
∵△PF1F2为直角三角形,
∴ =
= +
+
∴ =2c=
=2c= a,
a,
∴该椭圆的离心率e= =
= =
= (
( -1)=
-1)= -
- .
.
故选B.
点评:本题考查椭圆的简单性质,求得|F1F2|的长度是关键,也是难点,考查综合分析与运算的能力,属于难题.
解答:解:由椭圆的定义得:|PF1|+|PF2|=2a,|QF1|+|QF2|=2a,

∴△PQF2的周长为l=4a;
∵
 ,
, ,
,∴△PQF2为等腰直角三角形,设|PF2|=x,
则x+x+
 x=4a,
x=4a,∴x=
 =
= a,
a,∵|PF1|+|PF2|=2a,
∴|PF1|=2a-|PF2|=2a-
 a=
a= a,
a,∵△PF1F2为直角三角形,
∴
 =
= +
+
∴
 =2c=
=2c= a,
a,∴该椭圆的离心率e=
 =
= =
= (
( -1)=
-1)= -
- .
.故选B.
点评:本题考查椭圆的简单性质,求得|F1F2|的长度是关键,也是难点,考查综合分析与运算的能力,属于难题.

练习册系列答案
相关题目
 的焦点和上顶点分别为F1、F2、B,我们称△F1BF2为椭圆C的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比.
的焦点和上顶点分别为F1、F2、B,我们称△F1BF2为椭圆C的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比. 和
和 判断C2与C1是否相似,如果相似则求出C2与C1的相似比,若不相似请说明理由;
判断C2与C1是否相似,如果相似则求出C2与C1的相似比,若不相似请说明理由;
 与半椭圆
与半椭圆 组成的曲线称为“果圆”,其中a2=b2+c2,a>0,b>c>0.如图,设点F,F1,F2是相应椭圆的焦点,A1,A2和B1,B2是“果圆”与x,y轴的交点,
组成的曲线称为“果圆”,其中a2=b2+c2,a>0,b>c>0.如图,设点F,F1,F2是相应椭圆的焦点,A1,A2和B1,B2是“果圆”与x,y轴的交点, 的取值范围;
的取值范围;
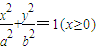 与半椭圆
与半椭圆 组成的曲线称为“果圆”,其中a2=b2+c2,a>0,b>c>0.如图,设点F,F1,F2是相应椭圆的焦点,A1,A2和B1,B2是“果圆”与x,y轴的交点,
组成的曲线称为“果圆”,其中a2=b2+c2,a>0,b>c>0.如图,设点F,F1,F2是相应椭圆的焦点,A1,A2和B1,B2是“果圆”与x,y轴的交点,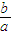 的取值范围;
的取值范围;