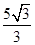题目内容
已知球的直径SC=4,A,B是该球球面上的两点,AB=2,∠ASC=∠BSC=45°,则棱锥S ABC的体积为( )
ABC的体积为( )
(A) 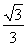 (B)
(B) 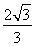 (C)
(C) 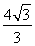 (D)
(D) 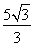
【答案】
C
【解析】如图所示,由题意知,在棱锥S ABC中,△SAC,△SBC都是等腰直角三角形,其中AB=2,SC=4,
ABC中,△SAC,△SBC都是等腰直角三角形,其中AB=2,SC=4,
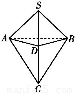
SA=AC=SB=BC=2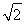 .取SC的中点D,易证SC垂直于面ABD,因此棱锥S
.取SC的中点D,易证SC垂直于面ABD,因此棱锥S ABC的体积为两个棱锥S
ABC的体积为两个棱锥S ABD和C
ABD和C ABD的体积和,所以棱锥S
ABD的体积和,所以棱锥S ABC的体积V=
ABC的体积V=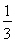 SC·S△ADB=
SC·S△ADB=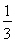 ×4×
×4×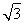 =
=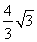 .
.

练习册系列答案
相关题目
已知球的直径SC=4,A,B是该球球面上的两点,AB=
,∠ASC=∠BSC=30°,则棱锥S-ABC的体积为( )
| 3 |
A、3
| ||
B、2
| ||
C、
| ||
| D、1 |
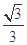 B.
B.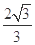 C.
C.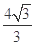 D.
D.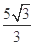
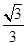 (B)
(B)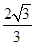
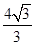 (D)
(D)