题目内容
已知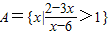 ,B={x|x2-2x+1-m2≤0,m>0},
,B={x|x2-2x+1-m2≤0,m>0},(1)若m=2,求A∩B;
(2)若A∪B=B,求实数m的取值范围.
【答案】分析:(1)把m=2代入可解得集合A、B,求交集即可;
(2)把A∪B=B转化为A⊆B,构建不等式组求解集可得m的取值范围.
解答:解:(1)由 得
得 ,解得2<x<6,∴A={x|2<x<6}(3分)
,解得2<x<6,∴A={x|2<x<6}(3分)
由m=2知x2-2x+1-m2≤0化为(x-3)(x+1)≤0,解得-1≤x≤3,
∴B={x|-1≤x≤3}(6分)
∴A∩B={x|2<x≤3}(7分)
(2)∵A∪B=B,∴A⊆B,(8分)
又∵m>0,∴不等式x2-2x+1-m2≤0的解集为1-m≤x≤1+m,(11分)
∴ 解得
解得 ,∴m≥5,∴实数m的取值范围是[5,+∞)(14分)
,∴m≥5,∴实数m的取值范围是[5,+∞)(14分)
点评:本题为不等式的解法,涉及集合的运算和转化的思想,属基础题.
(2)把A∪B=B转化为A⊆B,构建不等式组求解集可得m的取值范围.
解答:解:(1)由
 得
得 ,解得2<x<6,∴A={x|2<x<6}(3分)
,解得2<x<6,∴A={x|2<x<6}(3分)由m=2知x2-2x+1-m2≤0化为(x-3)(x+1)≤0,解得-1≤x≤3,
∴B={x|-1≤x≤3}(6分)
∴A∩B={x|2<x≤3}(7分)
(2)∵A∪B=B,∴A⊆B,(8分)
又∵m>0,∴不等式x2-2x+1-m2≤0的解集为1-m≤x≤1+m,(11分)
∴
 解得
解得 ,∴m≥5,∴实数m的取值范围是[5,+∞)(14分)
,∴m≥5,∴实数m的取值范围是[5,+∞)(14分)点评:本题为不等式的解法,涉及集合的运算和转化的思想,属基础题.

练习册系列答案
相关题目
 ,B={x|x2-2ax+a2-1>0},且A⊆B,求实数a的取值范围.
,B={x|x2-2ax+a2-1>0},且A⊆B,求实数a的取值范围.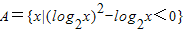 ,B={x|x2-2ax+a2-1>0},且A⊆B,求实数a的取值范围.
,B={x|x2-2ax+a2-1>0},且A⊆B,求实数a的取值范围.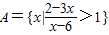 ,B={x|x2-2x+1-m2≤0,m>0},
,B={x|x2-2x+1-m2≤0,m>0},