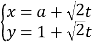题目内容
【题目】如图所示,在长方体![]() 中,
中,![]() ,点E是棱
,点E是棱![]() 上的一个动点,若平面
上的一个动点,若平面![]() 交棱
交棱![]() 于点
于点![]() ,给出下列命题:
,给出下列命题:
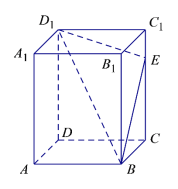
①四棱锥![]() 的体积恒为定值;
的体积恒为定值;
②存在点![]() ,使得
,使得![]() 平面
平面![]() ;
;
③对于棱![]() 上任意一点
上任意一点![]() ,在棱
,在棱![]() 上均有相应的点
上均有相应的点![]() ,使得
,使得![]() 平面
平面![]() ;
;
④存在唯一的点![]() ,使得截面四边形
,使得截面四边形![]() 的周长取得最小值.
的周长取得最小值.
其中真命题的是____________.(填写所有正确答案的序号)
【答案】①②④
【解析】
对①,将四棱锥![]() 分成两部分
分成两部分![]() 与
与![]() 分析即可
分析即可
对②,根据线面垂直的判定,注意用到![]() 再利用线面垂直与线线垂直的判定即可.
再利用线面垂直与线线垂直的判定即可.
对③,举出反例即可.
对④,四边形![]() 的周长
的周长![]() ,展开长方体分析最值即可.
,展开长方体分析最值即可.
对①,![]() ,又三棱锥
,又三棱锥![]() 底面
底面
![]() 不变,且因为
不变,且因为![]() ∥底面
∥底面![]() ,故
,故![]() 到底面
到底面![]() 的距离即
的距离即![]() 上的高长度不变.故三棱锥
上的高长度不变.故三棱锥![]() 体积一定,即四棱锥
体积一定,即四棱锥![]() 的体积恒为定值,①正确.
的体积恒为定值,①正确.
对②,因为![]() ,且长方体
,且长方体![]() ,故四边形
,故四边形![]() 为正方形,
为正方形,
故![]() .要
.要![]() 平面
平面![]() 则只需
则只需![]() ,又
,又![]() ,故只需
,故只需![]() 面
面![]() .
.
又![]() 平面
平面![]() ,故只需
,故只需![]() 即可.因为
即可.因为![]() ,故当
,故当![]() 时存在点
时存在点![]() ,使得
,使得![]() ,即
,即![]() 平面
平面![]() .故②正确.
.故②正确.
对③,当![]() 在
在![]() 时总有
时总有![]() 与平面
与平面![]() 相交,故③错误.
相交,故③错误.
对④,四边形![]() 的周长
的周长![]() ,分析
,分析![]() 即可.
即可.
将矩形![]() 沿着
沿着![]() 展开使得
展开使得![]() 在
在![]() 延长线上时,此时
延长线上时,此时![]() 的位置设为
的位置设为![]() ,则线段
,则线段![]() 与
与![]() 的交点即为使得截面四边形
的交点即为使得截面四边形![]() 的周长取得最小值时的唯一点
的周长取得最小值时的唯一点![]() .故④正确.
.故④正确.
故答案为:①②④

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目