题目内容
一物体作直线运动,其运动方程为S=| 1 |
| 4 |
| 5 |
| 3 |
分析:本题考查的是变化的快慢与变化率以及导数的综合应用类问题.在解答时,首先对函数求导,然后结合导数的几何意义,求导函数在t=0时的函数值即可获得问题的解答.
解答:解:由题意可知:
S′=t3-5t2+4t
由导函数的几何意义知:在t=0时刻的速度的大小即距离关于时间函数的导函数在t=0时的值.
又∵由t3-5t2+4t=0解得:
t=0或1或4
故答案为:0或1或4.
S′=t3-5t2+4t
由导函数的几何意义知:在t=0时刻的速度的大小即距离关于时间函数的导函数在t=0时的值.
又∵由t3-5t2+4t=0解得:
t=0或1或4
故答案为:0或1或4.
点评:本题考查的是变化的快慢与变化率以及导数的综合应用类问题.在解答的过程当中充分体现了导数的几何意义、求导的能力以及计算能力.值得同学们体会和反思,属基础题.

练习册系列答案
相关题目
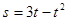 ,其中位移s单位为米,时间t的单
,其中位移s单位为米,时间t的单