题目内容
过抛物线y2=4x的焦点F作倾斜角为45°的直线交抛物线于A、B两点.(1)求AB的中点C到抛物线准线的距离；
(2)求线段AB的长.
解:(1)抛物线y2=4x的焦点坐标为(1，0)，准线方程为x=－1,
直线AB的方程为y=x－1,
设点A(x1,y1)、B(x2,y2).
将y=x－1代入y2=4x得x2－6x+1=0.
则x1+x2=6,x1·x2=1.
故中点C的横坐标为3.
所以中点C到准线的距离为3+1=4.
(2)|AB|=
=
=
=
=
=8,
即线段AB的长为8或记住类似这样条件的弦长|AB|=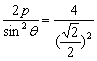
=8.
练习册系列答案
相关题目
倾斜角为
的直线过抛物线y2=4x的焦点且与抛物线交于A，B两点，则|AB|=（ ）
| π |
| 4 |
A、
| ||
B、8
| ||
| C、16 | ||
| D、8 |
过抛物线y2=4x的焦点F的直线交抛物线于A、B两点，点O是坐标原点，若|AF|=5，则△AOB的面积为（ ）
| A、5 | ||
B、
| ||
C、
| ||
D、
|