题目内容
阿亮与阿敏相约在19时至20时之间在某肯德基店见面,早到者到达后应等20分钟方可离去,假设两人到达的时刻是互不影响的,且在19时至20时之间的任何时刻到达相约地点都是等可能的,问他们两人见面的可能性有多大?
【答案】分析:由题意知本题是一个几何概型,试验包含的所有事件是Ω={(x,y)|0<x<1,0<y<1},做出事件对应的集合表示的面积,写出满足条件的事件是A={(x,y)|0<x<1,0<y<1,|x-y|< },算出事件对应的集合表示的面积,根据几何概型概率公式得到结果.
},算出事件对应的集合表示的面积,根据几何概型概率公式得到结果.
解答: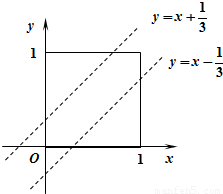 解:设阿亮与阿敏到达的时间分别为(19+x)时、(19+y)时,
解:设阿亮与阿敏到达的时间分别为(19+x)时、(19+y)时,
则0≤x≤1,0≤y≤1(2分)
若两人见面,则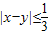 ,(2分)
,(2分)
如图,(2分)
正方形的面积为1,
落在两直线之间部分的面积为
∴两人见面的概率为 (2分)
(2分)
点评:本题是一个几何概型,对于这样的问题,一般要通过把试验发生包含的事件同集合结合起来,根据集合对应的图形做出面积,用面积的比值得到结果.
 },算出事件对应的集合表示的面积,根据几何概型概率公式得到结果.
},算出事件对应的集合表示的面积,根据几何概型概率公式得到结果.解答:
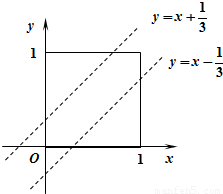 解:设阿亮与阿敏到达的时间分别为(19+x)时、(19+y)时,
解:设阿亮与阿敏到达的时间分别为(19+x)时、(19+y)时,则0≤x≤1,0≤y≤1(2分)
若两人见面,则
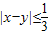 ,(2分)
,(2分)如图,(2分)
正方形的面积为1,
落在两直线之间部分的面积为

∴两人见面的概率为
 (2分)
(2分)点评:本题是一个几何概型,对于这样的问题,一般要通过把试验发生包含的事件同集合结合起来,根据集合对应的图形做出面积,用面积的比值得到结果.

练习册系列答案
相关题目