Question

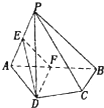（2013•泰安一模）如图，在四棱锥P-ABCD中，平面PAB⊥平面ABCD，AB=AD，∠BAD=60°，E，F分别是AP，AB的中点．求证：
（I）直线EF∥平面PBC；
（Ⅱ）平面DEF⊥平面PAB．

Answer 1

分析：（I）利用三角形的中位线定理和线面平行的判定定理即可得出；
（II）利用正三角形的判定和性质可得DF⊥AB，再利用面面垂直的性质和面面垂直的判定定理即可得出．

解答：证明：（I）在△PAB中，∵E，F分别是AP，AB的中点，∴EF∥PB，
又∵EF?平面PBC，PB?平面PBC，∴EF∥平面PBC；
（II）连接BD，∵AB=AD，∠BAD=60°，∴△ABD是正三角形，
∵F是AB的中点，∴DF⊥AB．
∵平面PAB⊥平面ABCD，平面PAB∩平面ABCD=AB，
∴DF⊥平面PAB，
又∵DF?平面DEF，∴平面PAB⊥平面DEF．

点评：熟练掌握三角形的中位线定理和线面平行的判定定理、正三角形的判定和性质、面面垂直的性质和面面垂直的判定定理是解题的关键．