Question

我们知道，对一个量用两种方法分别算一次，由结果相同可以构造等式，这是一种非常有用的思想方法--“算两次”（G．Fubini原理），如小学有列方程解应用题，中学有等积法求高…
请结合二项式定理，利用等式（1+x）ⁿ•（1+x）ⁿ=（1+x）²ⁿ（n∈N^*）
证明：
（1）；  
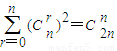（2）．

Answer 1

【答案】分析：（1）利用二项式定理系数的性质，求出xⁿ的系数，即可得到结论．
（2）利用已知关系式，求出等式两边x^m的系数，即可得到结果．
解答：证明：（1）考虑等式（1+x）ⁿ•（1+x）ⁿ=（1+x）²ⁿ，等式左边xⁿ的系数是=，
等式右边xⁿ的系数是，根据对应项系数相等得，=．（5分）
（2）仍考虑等式（1+x）ⁿ•（1+x）ⁿ=（1+x）²ⁿ，
等式左边x^m的系数是=，
等式右边x^m的系数是，根据对应项系数相等得，=．（10分）
点评：本题主要考查二项式定理等基础知识，考查推理论证能力．