题目内容
一几何体的三视图如图，其中侧（左）视图和俯视图都是腰长为4的等腰直角三角形，正（主）视图为直角梯形，则此几何体体积的大小为（ ）分析：由三视图确定该几何体的结构，然后利用体积公式求体积．
解答：
解：由三视图可知该几何体是一个放倒的四棱锥，其中棱锥的底面直角梯形如图，直角梯形ABCD为底，高为BE，其中底面直角梯形的底和高分别为，BC=4和AD=2，AB=4．锥体高BE=4．
所以四棱锥的体积为V=
×
×4=
×
×4=16．
故选B．
解：由三视图可知该几何体是一个放倒的四棱锥，其中棱锥的底面直角梯形如图，直角梯形ABCD为底，高为BE，其中底面直角梯形的底和高分别为，BC=4和AD=2，AB=4．锥体高BE=4．所以四棱锥的体积为V=
| 1 |
| 3 |
| (2+4)×4 |
| 2 |
| 1 |
| 3 |
| 6×4 |
| 2 |
故选B．
点评：本题考查三视图与直观图的关系，几何体的体积的求法，判断三视图复原的几何体的形状是解题的关键，
练习册系列答案
相关题目
一几何体的三视图如图所示，则该几何体的体积是（ ）
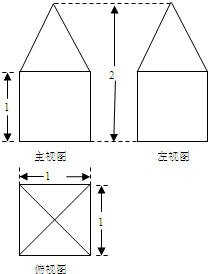
| A、2 | ||||
B、
| ||||
C、1+
| ||||
D、1+
|
已知一几何体的三视图如图，正视图和侧视图都是矩形，俯视图为正方形，在该几何体上任意选择5个顶点，它们可能是如下各种几何形体的5个顶点，这些几何形体是（写出所有正确结论的编号）
已知一几何体的三视图如图所示，则其体积为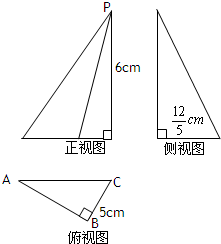
一几何体的三视图如图：
（2011•开封一模）已知一几何体的三视图如图，则该几何体外接球的表面积为