题目内容
 (2007•广州二模)如图所示,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AB=2,BC=1,AA1=
(2007•广州二模)如图所示,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AB=2,BC=1,AA1=| 3 |
(Ⅰ)证明:A1C⊥平面AB1C1;
(Ⅱ)若D是棱CC1的中点,在棱AB上是否存在一点E,使DE∥平面AB1C1,试证明你的结论.
分析:(Ⅰ)由已知可得BC⊥AC,BC⊥CC1,从而可证BC⊥平面ACC1A1,则BC⊥A1C;容易证明四边形ACC1A1为正方形,即证A1C⊥AC1,由线面垂直的判定定理可证
(Ⅱ)要使DE∥平面AB1C1,则根据面面平行的性质定理,只要证明平面EFD∥平面AB1C1,即证EF∥平面AB1C1,FD∥平面AB1C1,从而考虑,当点E为棱AB的中点时,取BB1的中点F,可证明
(Ⅱ)要使DE∥平面AB1C1,则根据面面平行的性质定理,只要证明平面EFD∥平面AB1C1,即证EF∥平面AB1C1,FD∥平面AB1C1,从而考虑,当点E为棱AB的中点时,取BB1的中点F,可证明
解答: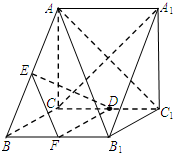 证明:(Ⅰ)∵∠ACB=90°,∴BC⊥AC.
证明:(Ⅰ)∵∠ACB=90°,∴BC⊥AC.
∵三棱柱ABC-A1B1C1为直三棱柱,
∴BC⊥CC1.
∵AC∩CC1=C,
∴BC⊥平面ACC1A1.
∵A1C?平面ACC1A1,∴BC⊥A1C
∵BC∥B1C1,则B1C1⊥A1C. …(4分)
在Rt△ABC中,AB=2,BC=1,
∴AC=
.
∵AA1=
,∴四边形ACC1A1为正方形.
∴A1C⊥AC1. …(6分)
∵B1C1∩AC1=C1,
∴A1C⊥平面AB1C1. …(7分)
(Ⅱ)当点E为棱AB的中点时,DE∥平面AB1C1 …(9分)
证明如下:
如图,取BB1的中点F,连EF、FD、DE,
∵D、E、F分别为CC1、AB、BB1的中点,
∴EF∥AB1.
∵AB1⊆平面AB1C1,EF?平面AB1C1
∴EF∥平面AB1C1. …(12分)
同理可证FD∥平面AB1C1.
∵EF∩FD=F,
∴平面EFD∥平面AB1C1
∵DE?平面EFD,
∴DE∥平面AB1C1. …(14分)
 证明:(Ⅰ)∵∠ACB=90°,∴BC⊥AC.
证明:(Ⅰ)∵∠ACB=90°,∴BC⊥AC.∵三棱柱ABC-A1B1C1为直三棱柱,
∴BC⊥CC1.
∵AC∩CC1=C,
∴BC⊥平面ACC1A1.
∵A1C?平面ACC1A1,∴BC⊥A1C
∵BC∥B1C1,则B1C1⊥A1C. …(4分)
在Rt△ABC中,AB=2,BC=1,
∴AC=
| 3 |
∵AA1=
| 3 |
∴A1C⊥AC1. …(6分)
∵B1C1∩AC1=C1,
∴A1C⊥平面AB1C1. …(7分)
(Ⅱ)当点E为棱AB的中点时,DE∥平面AB1C1 …(9分)
证明如下:
如图,取BB1的中点F,连EF、FD、DE,
∵D、E、F分别为CC1、AB、BB1的中点,
∴EF∥AB1.
∵AB1⊆平面AB1C1,EF?平面AB1C1
∴EF∥平面AB1C1. …(12分)
同理可证FD∥平面AB1C1.
∵EF∩FD=F,
∴平面EFD∥平面AB1C1
∵DE?平面EFD,
∴DE∥平面AB1C1. …(14分)
点评:本题主要考查空间中线面关系,考查数形结合的数学思想和方法,以及空间想象能力、逻辑推理能力和运算求解能力

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
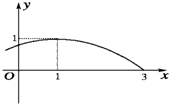 (2007•广州二模)函数f(x)=sin(ωx+?),(x∈R,ω>0,0≤?<2π)的部分图象如图所示,则ω=
(2007•广州二模)函数f(x)=sin(ωx+?),(x∈R,ω>0,0≤?<2π)的部分图象如图所示,则ω=
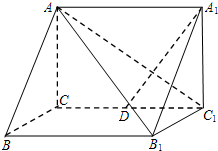 (2007•广州二模)如图所示,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AB=2,BC=1,
(2007•广州二模)如图所示,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AB=2,BC=1,