题目内容
（本小题满分12分）
设函数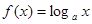
（
），已知数列
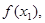
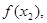
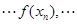是公差为2的等差数列，且
.
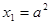（Ⅰ）求数列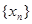
的通项公式；
（Ⅱ）当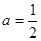
时，求证：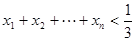
.
【答案】
（Ⅰ）
；（Ⅱ）见解析。
【解析】本试题主要是考查了舒蕾的通项公式的求解，以及数列的求和的证明
（1）因为
，则
得到结论。
（2）当
时，
，哪里用等比数列的求和公式得到结论，并证明。
解：（Ⅰ）
--------6分
（Ⅱ）当时，
----------12分
练习册系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
