题目内容
已知数列{an}满足an+1=2+(1)若a1=2,证明{bn}是等比数列;
(2)在(1)的条件下,求{an}的通项公式;
(3)若a1∈(![]() ,
,![]() ),证明数列{|cn|}的前n项和Sn满足Sn<1.
),证明数列{|cn|}的前n项和Sn满足Sn<1.
(1)证明:∵a1=2,∴b1=![]() =
=![]() .
.
由已知bn+1=![]() =
=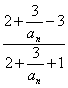 =
=![]() ·
·![]() =
=![]() bn,
bn,
∴{bn}是首项为![]() ,公比为
,公比为![]() 的等比数列.
的等比数列.
(2)解:由(1)知bn=(![]() )(
)(![]() )n-1=(
)n-1=(![]() )n,
)n,
即![]() =(
=(![]() )n,∴an=
)n,∴an=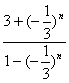 .
.
(3)证明:首先证明an>2.
①当n=1时,∵a1∈(![]() ,
,![]() ),∴a1>2;
),∴a1>2;
②假设n=k时,ak>2;
当n=k+1时,ak+1=2+![]() >2,
>2,
∴an>2.∴|![]() |<
|<![]() .
.
∴|cn|=|an-3|=|2+![]() -3|=|
-3|=|![]() |<
|<![]() |an-1-3|<
|an-1-3|<![]() |cn-1|.
|cn-1|.
∴|cn|<![]() |cn-1|<…<(
|cn-1|<…<(![]() )n-1|c1|.
)n-1|c1|.
∴Sn=|c1|+|c2|+…+|cn|<|c1|+![]() |c1|+…+(
|c1|+…+(![]() )n-1·|c1|
)n-1·|c1|
=|c1|·[1+(![]() )+…+(
)+…+(![]() )n-1]=|c1|·
)n-1]=|c1|·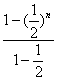
=2[1-(![]() )n]|c1|.
)n]|c1|.
∵![]() <a1<
<a1<![]() ,∴
,∴![]() <a1-3<
<a1-3<![]() ,即
,即![]() <c1<
<c1<![]() ,即|c1|<
,即|c1|<![]() .
.
∴Sn<2[1-(![]() )n]|c1|<1-(
)n]|c1|<1-(![]() )n<1.
)n<1.

练习册系列答案
相关题目