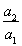题目内容
设Sn是公差不为0的等差数列{an}的前n项和,且S1,S2,S4成等比数列.(1)求
| a5 | a7 |
(2)若a5=3,求an及Sn的表达式.
分析:(1)要求
的值,可根据已知条件,求出公差d与首项a1的关系,将a5,a7都用公差d表示,约分即得答案.
(2)要求an及Sn的表达式,关键根据已知条件是列出公差d与首项a1的方程,解方程求出数列的基本项公差d与首项a1的值,然后根据定义即可求解.
| a5 |
| a7 |
(2)要求an及Sn的表达式,关键根据已知条件是列出公差d与首项a1的方程,解方程求出数列的基本项公差d与首项a1的值,然后根据定义即可求解.
解答:解:(1)设Sn的公差为d,
∵S1,S2,S4成等比,
∴,S22=S1S4
即(2a1+d)2=a1(4a1+6d),化简得d2=2a1d,
又d≠0,
∴d=2a1
0≤x≤3
∴
=
=
=
(2)∵a5=a1+4d=9a1=3,
∴a1=
,d=
an=a1+(n-1)d=
,
Sn=
n=
∵S1,S2,S4成等比,
∴,S22=S1S4
即(2a1+d)2=a1(4a1+6d),化简得d2=2a1d,
又d≠0,
∴d=2a1
0≤x≤3
∴
| a5 |
| a7 |
| a1+4d |
| a1+6d |
| 9d |
| 13d |
| 9 |
| 13 |
(2)∵a5=a1+4d=9a1=3,
∴a1=
| 1 |
| 3 |
| 2 |
| 3 |
an=a1+(n-1)d=
| 2n-1 |
| 3 |
Sn=
| a1+an |
| 2 |
| n2 |
| 3 |
点评:本题考查了等差与等比数列的基本概念和公式的应用,难度不大.牢固掌握教材所学过中的基本概念和公式就可以顺利解题啦.要求数列两项的比值,可根据已知条件,求出公差d与首项a1的关系,将两项都用公差d表示,约分即得答案.(如本题第(1)步).要求an及Sn的表达式,关键根据已知条件是列出公差d与首项a1的方程,解方程求出数列的基本项公差d与首项a1的值,然后根据定义即可求解.方程思想是解决数列问题的基本思想,通过公差列方程(组)来求解基本量是数列中最基本的方法,同时在解题中也要注意数列性质的应用.

练习册系列答案
相关题目
设Sn是公差不为0的等差数列{an}的前n项和,且S1,S2,S4成等比数列,则
等于( )
| a2 |
| a1 |
| A、1 | B、2 | C、3 | D、4 |