题目内容
某市规定,高中学生三年在校期间参加不少于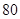 小时的社区服务才合格.教育部门在全市随机抽取200位学生参加社区服务的数据,按时间段
小时的社区服务才合格.教育部门在全市随机抽取200位学生参加社区服务的数据,按时间段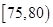 ,
, ,
,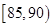 ,
,
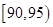 ,
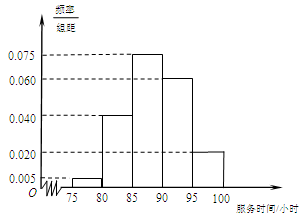
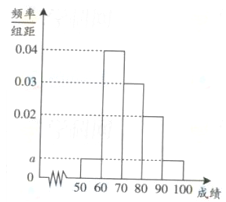
,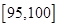 (单位:小时)进行统计,其频率分布直方图如图所示.
(单位:小时)进行统计,其频率分布直方图如图所示.
(Ⅰ)求抽取的200位学生中,参加社区服务时间不少于90小时的学生人数,并估计
从全市高中学生中任意选取一人,其参加社区服务时间不少于90小时的概率;
(Ⅱ)从全市高中学生(人数很多)中任意选取3位学生,记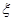 为3位学生中参加社区服务时间不少于90小时的人数.试求随机变量
为3位学生中参加社区服务时间不少于90小时的人数.试求随机变量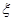 的分布列和数学期望
的分布列和数学期望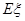 .
.
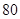 小时的社区服务才合格.教育部门在全市随机抽取200位学生参加社区服务的数据,按时间段
小时的社区服务才合格.教育部门在全市随机抽取200位学生参加社区服务的数据,按时间段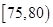 ,
, ,
,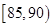 ,
,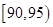 ,
,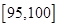 (单位:小时)进行统计,其频率分布直方图如图所示.
(单位:小时)进行统计,其频率分布直方图如图所示.(Ⅰ)求抽取的200位学生中,参加社区服务时间不少于90小时的学生人数,并估计
从全市高中学生中任意选取一人,其参加社区服务时间不少于90小时的概率;
(Ⅱ)从全市高中学生(人数很多)中任意选取3位学生,记
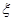 为3位学生中参加社区服务时间不少于90小时的人数.试求随机变量
为3位学生中参加社区服务时间不少于90小时的人数.试求随机变量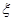 的分布列和数学期望
的分布列和数学期望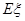 .
.
(Ⅰ) (Ⅱ)
(Ⅱ)
 (Ⅱ)
(Ⅱ)
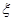 | 0 | 1 | 2 | 3 |
 |  |  |  |  |
试题分析:(Ⅰ)根据频率分布直方图中小长方形面积为频率,而频数为总数与频率之积. 因此参加社区服务时间在时间段
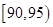 小时的学生人数为
小时的学生人数为 (人),参加社区服务时间在时间段
(人),参加社区服务时间在时间段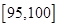 小时的学生人数为
小时的学生人数为 (人).所以抽取的200位学生中,参加社区服务时间不少于90小时的学生人数为
(人).所以抽取的200位学生中,参加社区服务时间不少于90小时的学生人数为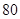 人.概率估计为
人.概率估计为 (Ⅱ)随机变量
(Ⅱ)随机变量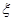 的可能取值为
的可能取值为 .由(Ⅰ)可知,概率为
.由(Ⅰ)可知,概率为 因为
因为 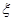 ~
~ ,所以
,所以 .随机变量
.随机变量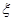 的分布列为
的分布列为 | 0 | 1 | 2 | 3 |
 |  |  |  |  |
解:(Ⅰ)根据题意,
参加社区服务时间在时间段
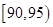 小时的学生人数为
小时的学生人数为 (人),
(人),参加社区服务时间在时间段
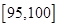 小时的学生人数为
小时的学生人数为 (人).
(人).所以抽取的200位学生中,参加社区服务时间不少于90小时的学生人数为
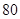 人.
人.所以从全市高中学生中任意选取一人,其参加社区服务时间不少于90小时的
概率估计为
 5分
5分(Ⅱ)由(Ⅰ)可知,从全市高中生中任意选取1人,其参加社区服务时间不少于90小时的概率为

由已知得,随机变量
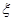 的可能取值为
的可能取值为 .
.所以
 ;
; ;
; ;
; .
.随机变量
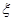 的分布列为
的分布列为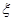 | 0 | 1 | 2 | 3 |
 |  |  |  |  |
因为
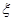 ~
~ ,所以
,所以 . 13分
. 13分
练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目


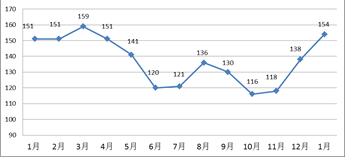
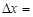 本月价格指数
本月价格指数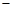 上月价格指数.规定:当
上月价格指数.规定:当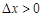 时,称本月价格指数环比增长;
时,称本月价格指数环比增长;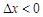 时,称本月价格指数环比下降;当
时,称本月价格指数环比下降;当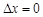 时,称本月价格指数环比持平.
时,称本月价格指数环比持平. ,
, ”是“(x0,y0)满足线性回归方程y=bx+a”的( )
”是“(x0,y0)满足线性回归方程y=bx+a”的( )