题目内容
如图,棱长为2的正方体ABCD—A1B1C1D1中,E、F、M、N分别是A1B1、BC、C1D1、B1C1的中点.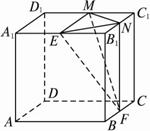
(1)求证:平面MNF⊥平面ENF.
(2)在EF上求一点H使平面MNH⊥平面EFM.
(1)证明:易证MN⊥FN,又N是B1C1的中点,故△MNE是等腰直角三角形.?
∴∠MNE=90°.∴MN⊥NE.?
∴MN⊥面ENF.?
∴面MNF⊥面ENF.?
(2)解析:过N作NH⊥EF于H,连结MH,则MH⊥EF.?
∴EF⊥面MNH.故面EFM⊥面MNH.?
∵∠ENF=90°,NE=![]() ,EF=
,EF=![]() ,?
,?
∴EH=![]() .
.

练习册系列答案
相关题目
 现有一块棱长为a的正方体形的木料,如图,M、N、P分别为AD、CD、BB1的中点.现要沿过M、N、P三点的平面将木料锯开.
现有一块棱长为a的正方体形的木料,如图,M、N、P分别为AD、CD、BB1的中点.现要沿过M、N、P三点的平面将木料锯开. 内(含正方体表面)任取一点
内(含正方体表面)任取一点 ,则
,则 的概率
的概率 ( )
( )

 B.
B. C.
C. D.
D.
 内有一个内切球O,则过棱
内有一个内切球O,则过棱 和
和 的中点
的中点 、
、 的直线与球面交点为
的直线与球面交点为 、
、 ,则
,则 A.
A. B.
B. C.
C. D.
D. 
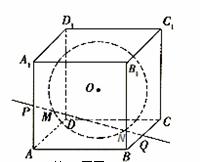 如图,在棱长为2的正方体
如图,在棱长为2的正方体 内有一个内切球O,则过棱
内有一个内切球O,则过棱 和
和 的中点
的中点 、
、 的直线与球面交点为
的直线与球面交点为 、
、 ,则
,则 B.
B.
 D.
D.
 如图,在棱长为2的正方体
如图,在棱长为2的正方体