题目内容
设F1、F2分别是椭圆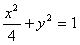 的左、右焦点。
的左、右焦点。
(1)若P是该椭圆上的一个动点,求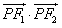 的取值范围;
的取值范围;
(2)设过定点Q(0,2)的直线l与椭圆交于不同的两点M、N,且∠MON为锐角(其中O为坐标原点),求直线l的斜率k的取值范围;
(3)设A(2,0),B(0,1)是它的两个顶点,直线y=kx(k>0)与AB相交于点D,与椭圆相交于E、F两点,求四边形AEBF面积的最大值。
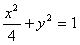 的左、右焦点。
的左、右焦点。(1)若P是该椭圆上的一个动点,求
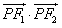 的取值范围;
的取值范围; (2)设过定点Q(0,2)的直线l与椭圆交于不同的两点M、N,且∠MON为锐角(其中O为坐标原点),求直线l的斜率k的取值范围;
(3)设A(2,0),B(0,1)是它的两个顶点,直线y=kx(k>0)与AB相交于点D,与椭圆相交于E、F两点,求四边形AEBF面积的最大值。
解:(1)易知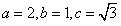 ,
,
所以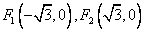 ,
,
设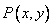 ,则
,则
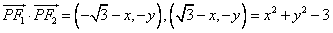
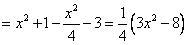 ,
,
故 。
。
(2)显然直线x=0不满足题设条件,
可设直线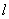 :
: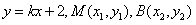 ,
,
联立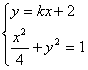 ,
,
消去y,整理得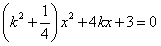 ,
,
∴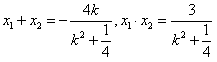 ,
,
由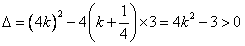 ,解得:
,解得: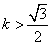 或
或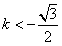 , ①
, ①
又0°<∠MON<90° cos∠MON>0
cos∠MON>0
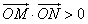 ,
,
∴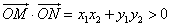 ,
,
又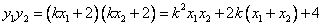
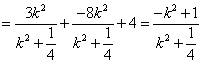 ,
,
∵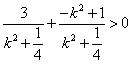 ,即
,即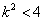 ,
,
∴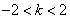 , ②
, ②
故由①、②得 或
或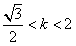 。
。
(3)根据点到直线的距离公式和①式知,点E,F到AB的距离分别为
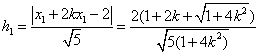 ,
,
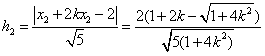 ,
,
又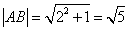 ,
,
所以,四边形AEBF的面积为
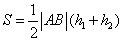
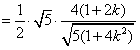
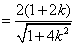
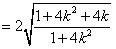
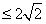 ,
,
当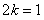 即
即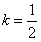 时,等号成立,所以S的最大值为
时,等号成立,所以S的最大值为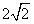 。
。
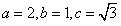 ,
,所以
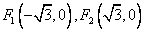 ,
,设
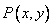 ,则
,则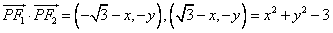
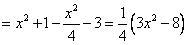 ,
,故
 。
。(2)显然直线x=0不满足题设条件,
可设直线
 :
: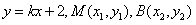 ,
,联立
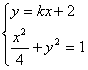 ,
,消去y,整理得
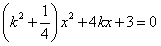 ,
,∴
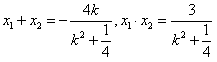 ,
,由
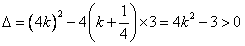 ,解得:
,解得: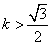 或
或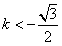 , ①
, ①又0°<∠MON<90°
 cos∠MON>0
cos∠MON>0
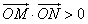 ,
,∴
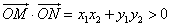 ,
,又
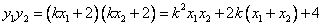
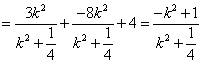 ,
,∵
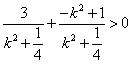 ,即
,即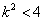 ,
,∴
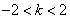 , ②
, ②故由①、②得
 或
或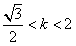 。
。(3)根据点到直线的距离公式和①式知,点E,F到AB的距离分别为
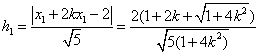 ,
,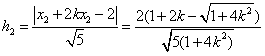 ,
,又
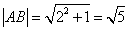 ,
,所以,四边形AEBF的面积为
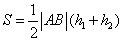
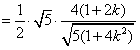
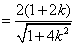
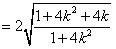
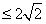 ,
,当
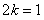 即
即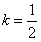 时,等号成立,所以S的最大值为
时,等号成立,所以S的最大值为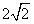 。
。
练习册系列答案
相关题目
 已知椭圆
已知椭圆 的左、右焦点,其右焦点是直线y=x-1与x轴的交点,短轴的长是焦距的2倍.
的左、右焦点,其右焦点是直线y=x-1与x轴的交点,短轴的长是焦距的2倍. 的最大值和最小值;
的最大值和最小值; 的左、右焦点,P为椭圆上任一点,点M的坐标为(6,4),则|PM|+|PF1|的最大值为
.
的左、右焦点,P为椭圆上任一点,点M的坐标为(6,4),则|PM|+|PF1|的最大值为
.