题目内容
设函数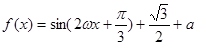 (其中0<
(其中0<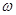 <1,
<1,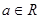 ),且
),且 的图象在y轴右侧的第一个最高点横坐标为
的图象在y轴右侧的第一个最高点横坐标为 ,且在区间
,且在区间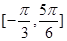 上的最小值为
上的最小值为 ,则a=( )
,则a=( )
| A.1 | B.2 | C.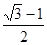 | D.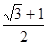 |
D
解析试题分析:既然在 处取得第一个最高点,那么有2
处取得第一个最高点,那么有2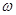 ×
× +
+ =
= ,
,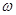 =
=
所以,f(x)=sin(x+ )+a+
)+a+ ,f(x)在区间
,f(x)在区间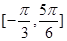 上的最小值为
上的最小值为 ,
,
当x在区间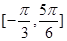 时,x+
时,x+ 在区间[0,
在区间[0, ]里,在这个区间内,当x+
]里,在这个区间内,当x+ =
= 时,取得最小值。即此时f(x)的最小值为a+
时,取得最小值。即此时f(x)的最小值为a+ -
- =
= ,故有
,故有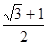 ,选D.
,选D.
考点:正弦型函数的图象和性质
点评:中档题,关键是确定角的范围,进一步求得三角函数值的范围,得到a的方程。

练习册系列答案
相关题目
函数 的最小正周期是( )
的最小正周期是( )
A. | B. | C. | D. |
为得到函数 的图象, 只需要将函数
的图象, 只需要将函数 的图象向( ) 个单位
的图象向( ) 个单位
A.左平移 | B.右平移 |
C.左平移 | D.右平移 |
如果函数 的图像关于点
的图像关于点 中心对称,那么
中心对称,那么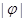 的最小值为( )
的最小值为( )
A. | B. | C. | D. |
现有四个函数:① ②
② ③
③ ④
④ 的图象(部分)如下,但顺序被打乱,则按照从左到右将图象对应的函数序号安排正确的一组是( )
的图象(部分)如下,但顺序被打乱,则按照从左到右将图象对应的函数序号安排正确的一组是( )
| A.④①②③ | B.①④③② | C.①④②③ | D.③④②① |
函数 图象的两条相邻对称轴间的距离为
图象的两条相邻对称轴间的距离为
A. | B. | C. | D. |
 ,将函数
,将函数 的图像向左平移
的图像向左平移 (
( )个单位,所得图像对应的函数为偶函数,则
)个单位,所得图像对应的函数为偶函数,则



 =
= .将函数
.将函数 的图象向左平移
的图象向左平移 个单位,以下是所得函数图象的一个对称中心是
个单位,以下是所得函数图象的一个对称中心是 



 x
x
 x)的图象向右平移
x)的图象向右平移 (
( 0)个单位,使得平移后的图象仍过点(
0)个单位,使得平移后的图象仍过点( ,
, ),则
),则
