题目内容
 已知函数f(x)=Asin(ωx+?)
已知函数f(x)=Asin(ωx+?)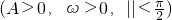 的部分图象如图所示,若函数y=g(x)的图象与函数y=f(x)的图象关于直线
的部分图象如图所示,若函数y=g(x)的图象与函数y=f(x)的图象关于直线 对称.
对称.
(1)求函数g(x)的解析式;
(2)若关于x的方程3[g(x)]2-mg(x)+1=0在区间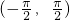 上有解,求实数m的取值范围;
上有解,求实数m的取值范围;
(3)令F(x)=f(x)+g(x),x∈[0,π],求函数F(x)的值域.
解:(1)由图可知,A=1,
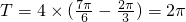 ,∴ω=1,
,∴ω=1,
即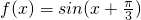 .
.
∴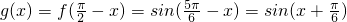 .
.
(2)∵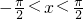 ,
,
∴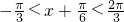 ,
,
∴ .
.
又3[g(x)]2-mg(x)+1=0,
∴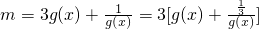 ,
,
①当g(x)=0时,m∈φ;
②当 时,
时,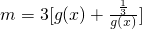 =
=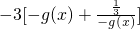 ≤-3×2
≤-3×2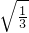 =-2
=-2
∴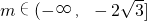 ;
;
③当0<g(x)≤1时,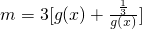 ≥3×2
≥3×2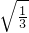 =2
=2
∴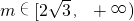 .
.
综上,实数m的取值范围是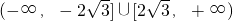 .
.
(3)∵F(x)=f(x)+g(x),
∴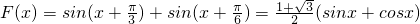 =
= .
.
又x∈[0,π],∴ ,
,
∴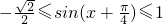 ,
,
即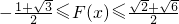 ,
,
∴函数函数F(x)的值域为 .
.
分析:(1)利用函数图象先求函数的振幅和周期,再确定初相φ的值,最后利用函数图象的对称性,求得函数g(x)的解析式即可
(2)先求函数g(x)在区间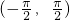 上的值域,再将方程有解问题转化为求函数
上的值域,再将方程有解问题转化为求函数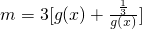 ,
, 的值域问题,利用均值定理即可求得函数值域;
的值域问题,利用均值定理即可求得函数值域;
(3)先利用三角变换公式将函数F(x)的解析式化简为y=Asin(ωx+φ)型函数,再利用正弦函数的图象和性质求函数值域即可
点评:本题主要考查了y=Asin(ωx+φ)型函数的图象和性质,三角变换公式在化简和求值中的应用,均值定理求函数最值的方法,属中档题
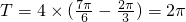 ,∴ω=1,
,∴ω=1,即
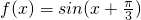 .
.∴
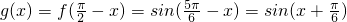 .
.(2)∵
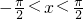 ,
,∴
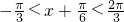 ,
,∴
 .
.又3[g(x)]2-mg(x)+1=0,
∴
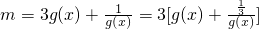 ,
,①当g(x)=0时,m∈φ;
②当
 时,
时,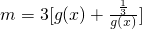 =
=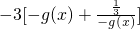 ≤-3×2
≤-3×2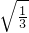 =-2
=-2
∴
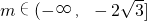 ;
;③当0<g(x)≤1时,
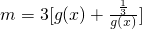 ≥3×2
≥3×2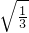 =2
=2
∴
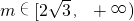 .
.综上,实数m的取值范围是
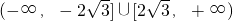 .
.(3)∵F(x)=f(x)+g(x),
∴
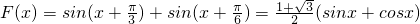 =
= .
.又x∈[0,π],∴
 ,
,∴
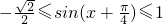 ,
,即
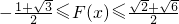 ,
,∴函数函数F(x)的值域为
 .
.分析:(1)利用函数图象先求函数的振幅和周期,再确定初相φ的值,最后利用函数图象的对称性,求得函数g(x)的解析式即可
(2)先求函数g(x)在区间
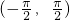 上的值域,再将方程有解问题转化为求函数
上的值域,再将方程有解问题转化为求函数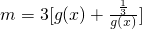 ,
, 的值域问题,利用均值定理即可求得函数值域;
的值域问题,利用均值定理即可求得函数值域;(3)先利用三角变换公式将函数F(x)的解析式化简为y=Asin(ωx+φ)型函数,再利用正弦函数的图象和性质求函数值域即可
点评:本题主要考查了y=Asin(ωx+φ)型函数的图象和性质,三角变换公式在化简和求值中的应用,均值定理求函数最值的方法,属中档题

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目