题目内容
已知命题p：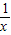
＞0；命题q：
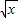有意义，则¬p是¬q的（ ）A．充分不必要条件
B．必要不充分条件
C．充分必要条件
D．不充分不必要条件
【答案】分析：解不等式
＞0，易得¬p对应x的取值范围，根据函数定义域的求法，易得到条件q：
有意义，得¬q对应x的取值范围，然后易判断p⇒¬q，¬q⇒¬p的真假，最后根据充要条件的定义，得到答案．
解答：解：∵p：
＞0⇒x＞0，
∴¬p：x≤0．
又∵q：
有意义⇒x≥0，
∴¬q：x＜0，
∴¬p⇒¬q为假命题，但¬q⇒¬p为真命题，
∴¬p是¬q的必要不充分条件．
故选B
点评：本题考查的知识点是充要条件的定义，先判断p⇒¬q，¬q⇒¬p的真假，最后根据充要条件的定义，得到答案是解答本题的关键．
＞0，易得¬p对应x的取值范围，根据函数定义域的求法，易得到条件q：有意义，得¬q对应x的取值范围，然后易判断p⇒¬q，¬q⇒¬p的真假，最后根据充要条件的定义，得到答案．解答：解：∵p：
＞0⇒x＞0，∴¬p：x≤0．
又∵q：
有意义⇒x≥0，∴¬q：x＜0，
∴¬p⇒¬q为假命题，但¬q⇒¬p为真命题，
∴¬p是¬q的必要不充分条件．
故选B
点评：本题考查的知识点是充要条件的定义，先判断p⇒¬q，¬q⇒¬p的真假，最后根据充要条件的定义，得到答案是解答本题的关键．
练习册系列答案
相关题目
已知命p：?x∈R，使得x+
＜2，命题q：?x∈R，x2+x+1＞0，下列结论正确的是（ ）
| 1 |
| x |
| A、命题“p∧q”是真命题 |
| B、命题“（￢p）∧q”是真命题 |
| C、命题“p∧（￢q）”是真命题 |
| D、命题“（￢p）∧（￢q）”是真命题 |
，命题q：?x∈R，x2+x+1＞0，下列结论正确的是（ ）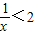
，命题q：?x∈R，x2+x+1＞0，下列结论正确的是（ ）
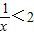，命题q：?x∈R，x2+x+1＞0，下列结论正确的是（ ）
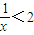，命题q：?x∈R，x2+x+1＞0，下列结论正确的是（ ）