题目内容
与直线l : y=2x+3平行,且与圆x2+y2-2x-4y+4=0相切的直线方程是( ).
A.x-y±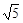 =0 =0 | B.2x-y+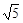 =0 =0 |
C.2x-y-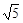 =0 =0 | D.2x-y±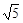 =0 =0 |
D
解析试题分析:解:∵直线l:y=2x+3∴kl=2若圆x2+y2-2x-4y+4=0的切线与l平行所以切线的斜率k=2观察四个答案; A中直线的斜率为1,不符合条件,故A错误; B中直线的斜率为 ,不符合条件,故B错误; C中直线的斜率为-2,不符合条件,故C错误; D中直线的斜率为2,符合条件,故D正确;故选D
,不符合条件,故B错误; C中直线的斜率为-2,不符合条件,故C错误; D中直线的斜率为2,符合条件,故D正确;故选D
考点:直线平行
点评:两条直线平行,则两直线的斜率相等,截距不等,即:l1∥l2?k1=k2, b1≠b2

练习册系列答案
相关题目
如果两条直线l1: 与l2:
与l2: 平行,那么
平行,那么 等于( )
等于( )
A.2或 | B.2 | C. | D. |
垂直于直线y=x+1且与圆x2+y2=1相切于第一象限的直线方程是 ( )
A.x+y- =0 =0 | B.x+y+1=0 |
| C.x+y-1=0 | D.x+y+ =0 =0 |
若点 为圆
为圆 的弦
的弦 的中点,则直线
的中点,则直线 的方程是( )
的方程是( )
A. | B. |
C. | D. |
若直线的参数方程为 ,则直线的斜率为( )
,则直线的斜率为( )
A. | B. | C. | D. |
已知直线 过点(0,7),且与直线
过点(0,7),且与直线 平行,则直线
平行,则直线 的方程为( ).
的方程为( ).
A. | B. |
C. | D. |
图中的直线l1、l2、l3的斜率分别为k1、k2、k3,则 ( )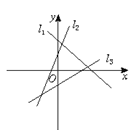
| A.k1<k2<k3 | B.k3<k1<k2 | C.k3<k2<k1 | D.k1<k3<k2 |
已知直线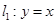 ,若直线
,若直线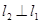 ,则直线
,则直线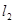 的倾斜角为
的倾斜角为
A.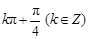 | B.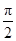 | C.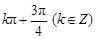 | D.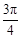 |
过点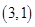 作圆
作圆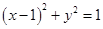 的两条切线,切点分别为
的两条切线,切点分别为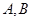 ,则直线
,则直线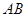 的方程为( )
的方程为( )
A.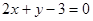 | B.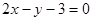 |
C.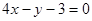 | D.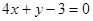 |