Question

设椭圆C：

x2

a2

+

y2

b2

=1(a＞b＞0)的左、右焦点分别为F₁、F₂，点P在椭圆上且在x轴上方，|PF1|=7，|PF2|=5，cos∠F1F2P=

1

5

．
（1）求椭圆C的方程；
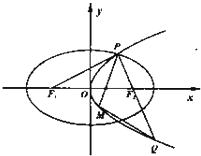
（2）抛物线D：y²=4mx（m＞0）过点P，连接PF₂并延长与抛物线D交于点Q，M是抛物线D上一动点（且M在P与Q之间运动），求△MPQ面积的最大值．

Answer 1

分析：（1）2a=||PF₁|+|PF₂|=7+5=12，a=6，由cos∠F1F2P=

1

5

，|PF₂|=5，得2c=|F₁F₂|=1+5=6，c=3，由此能求出椭圆C的方程．
（2）由（1）知，点P的坐标为（2，2

6

），抛物线D：y²=4mx（m＞0）过点P，故抛物线D：y²=12x．由P（2，2

6

），F₂（3，0），得直线PF₂的方程为y=-2

6

x+6

6

，联立

y2=12x y=-2 6 x+6 6

，得2x²-13x+18=0，解得P（2，2

6

），Q（

9

2

，-3

6

），先求出|PQ|，再求出M到直线y=-2

6

x+6

6

的最大距离，由此能求出△MPQ面积的最大值．

解答：解：（1）2a=||PF₁|+|PF₂|=7+5=12，a=6，
如图，过P点作PO⊥x轴，交x轴与点O，

∵cos∠F1F2P=

1

5

，|PF₂|=5，
∴|OF₁|=1，∴|PO|=

25-1

=2

6

，
∵|PF₁|=7，∴|F₁O|=

49-24

=5，
2c=|F₁F₂|=1+5=6，c=3，
b²=a²-c²=25-9=16，
∴椭圆C的方程是

x2

25

+

y2

16

=1．
（2）由（1）知，点P的坐标为（2，2

6

），
∵抛物线D：y²=4mx（m＞0）过点P，
∴24=16m，解得m=3，∴抛物线D：y²=12x．
∵P（2，2

6

），F₂（3，0），
∴直线PF₂的方程为：

y

x-3

=

2 6

2-3

，即y=-2

6

x+6

6

，
联立

y2=12x y=-2 6 x+6 6

，消去y，并整理，得2x²-13x+18=0，
解得x=2，或x=

9

2

，
∴P（2，2

6

），Q（

9

2

，-3

6

），|PQ|=

(2- 9 2 )2+(2 6 +3 6 )2

=

25

4

．
设M（x，

12x

），∵M在P与Q之间运动，∴0≤x≤

9

2

，0≤

x

≤

3 2

2

，
则M到直线y=-2

6

x+6

6

的距离d=

|2 6 x+ 12x -6 6 |

5

=

6

5

|2x+

2

x

-6|，
∴当

x

=

3 2

2

时，dmax=

6

5

|9+3-6|=

6 6

5

，
∴△MPQ面积的最大值S=

1

2

×

25

4

×

6 6

5

=

15 6

4

．

点评：本题考查直线与圆锥曲线的综合问题，解题时要认真审题，仔细解答，注意挖掘题设中的隐含条件．本题主要考查运算，整个题目的解答过程看起来非常繁琐，注意运算．