题目内容
已知函数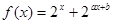 ,且
,且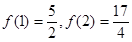
(1)求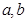 ;
;
(2)判断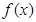 的奇偶性;
的奇偶性;
(3)判断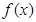 在
在 上的单调性,并证明。
上的单调性,并证明。
【答案】
(1)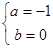 ; (2)
; (2) 为偶函数;(3)
为偶函数;(3) 在
在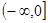 单调递减。
单调递减。
【解析】
试题分析:(1).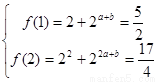 ,
,  解得:
解得: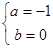
(2)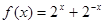 ,定义域为
,定义域为
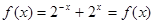 ,所以
,所以 为偶函数
为偶函数
(3)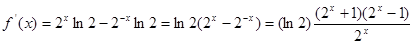
由 ,
, ,则
,则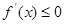 ,则
,则 在
在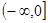 单调递减
单调递减
考点:指数函数的性质,函数的奇偶性、单调性,应用导数研究函数的单调性。
点评:中档题,本题解答思路明确,通过布列方程组求得a,b的值。判断函数的奇偶性,主要应用奇偶函数的定义。在某区间,导数值非负,函数为增函数,导数值非正,函数为减函数。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 ,且
,且
 的值
的值 上的单调性,并利用定义给出证明
上的单调性,并利用定义给出证明 ,且
,且 .
. 的奇偶性并说明理由;
的奇偶性并说明理由;
 上的单调性,并证明你的结论;
上的单调性,并证明你的结论; 上,不等式
上,不等式 恒成立,试确定实数
恒成立,试确定实数 的取值范围.
的取值范围. ,且
,且
 的表达式;
的表达式; 的项满足
的项满足 ,试求
,试求 ;
;