题目内容
已知函数f(x)=(cosx+sinx)(cosx-sinx).(1)求函数f(x)的最小正周期;
(2)若
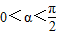 ,
,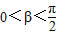 ,且
,且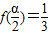 ,
,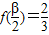 ,求sin(α-β)的值.
,求sin(α-β)的值.
【答案】分析:(1)利用二倍角公式化简函数表达式,直接求出函数的周期.
(2)若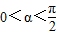 ,
,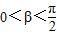 ,且
,且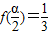 ,
,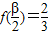 ,求sin(α-β)的值.
,求sin(α-β)的值.
解答:解:(1)函数f(x)=(cosx+sinx)(cosx-sinx)=cos2x.
所以T=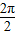 =π.
=π.
(2)若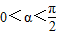 ,
,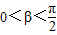 ,且
,且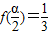 ,
,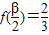 ,
,
所以cosα= ,cosβ=
,cosβ= ,
,
所以sinα=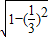 =
=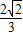 ,
,
sinβ=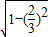 =
=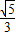 ,
,
所以sin(α-β)=sinαosβ-cosαsinβ=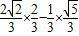 =
=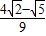 .
.
点评:本题考查二倍角公式的应用,两角差的正弦函数的应用,考查计算能力.
(2)若
 ,
,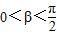 ,且
,且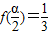 ,
,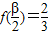 ,求sin(α-β)的值.
,求sin(α-β)的值.解答:解:(1)函数f(x)=(cosx+sinx)(cosx-sinx)=cos2x.
所以T=
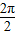 =π.
=π.(2)若
 ,
,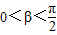 ,且
,且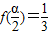 ,
,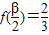 ,
,所以cosα=
 ,cosβ=
,cosβ= ,
,所以sinα=
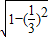 =
=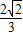 ,
,sinβ=
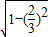 =
=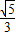 ,
,所以sin(α-β)=sinαosβ-cosαsinβ=
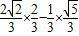 =
=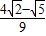 .
.点评:本题考查二倍角公式的应用,两角差的正弦函数的应用,考查计算能力.

练习册系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|