题目内容
已知球面的三个大圆所在平面两两垂直,则以三个大圆的交点为顶点的八面体的体积与球体积之比是( )A.1:π
B.1:2π
C.2:π
D.4:3π
【答案】分析:设出球的半径,说明正八面体分成两个正四棱锥,求出底面边长和高,求出正八面体的体积,球的体积,即可得到比值.
解答:解:设球的半径为R,把正八面体分成两个正四棱锥,
四棱锥的底面的正方形的对角线长2R,可得正方形边长为 R,
R,
底面正方形面积为2R2,
四棱锥的高为R,
正八面体的体积为: 2R2•2R=
2R2•2R= R3
R3
所以正八面体的体积与球体积之比为:
( R3):(
R3):( πR3)=1:π
πR3)=1:π
故选A.
点评:本题是基础题,考查球的内接多面体,分析出正八面体是两个正四棱锥,正确利用球的半径,求出相关数据,是解好本题的关键,考查空间想象能力,计算能力.
解答:解:设球的半径为R,把正八面体分成两个正四棱锥,
四棱锥的底面的正方形的对角线长2R,可得正方形边长为
 R,
R,底面正方形面积为2R2,
四棱锥的高为R,
正八面体的体积为:
 2R2•2R=
2R2•2R= R3
R3所以正八面体的体积与球体积之比为:
(
 R3):(
R3):( πR3)=1:π
πR3)=1:π故选A.
点评:本题是基础题,考查球的内接多面体,分析出正八面体是两个正四棱锥,正确利用球的半径,求出相关数据,是解好本题的关键,考查空间想象能力,计算能力.

练习册系列答案
相关题目
已知球面的三个大圆所在平面两两垂直,则以三个大圆的交点为顶点的八面体的体积与球体积之比是( )
| A、1:π | B、1:2π | C、2:π | D、4:3π |
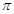 B.1 : 2
B.1 : 2 B.1:2
B.1:2 C.1
C.1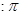 D.4:3
D.4:3