题目内容

在△ABC中，
cosA
b
=
cosB
a
，则△ABC的形状是______．
∵
cosA
b
=
cosB
a

由正弦定理可得，
sinCcosA
sinB
=
sinCcosB
sinA

三角形中，sinC≠0
∴
cosA
sinB
=
cosB
sinA

即sinAcosA=sinBcosB
∴sin2A=sin2B
则有2A=2B或2A+2B=π
∴A=B  或A+B=
π
2

故答案为：等腰三角形或直角三角形
练习册系列答案
相关题目
6、在△ABC中，cos（A-B）+sin（A+B）=2，则△ABC的形状为
等腰直角
三角形．
3、在△ABC中，cos 2B＞cos 2A是A＞B的（　　）
在△ABC中，cos(A+C)=-
3
5
，且a，c的等比中项为
35
．
（1）求△ABC的面积；
（2）若a=7，求角C．
在△ABC中，cos(A-C)+2cos2
B
2
=
5
2
，三边a，b，c成等比数列，求B．
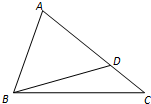精英家教网如图，在△ABC中，cos∠ABC=
1
3
，AB=6，AD=2DC，点D在AC边上．
（Ⅰ）若BC=AC，求sin∠ADB；
（Ⅱ）若BD=4
3
，求BC的长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网