题目内容
已知函数f（x）=cos2（x+
），g（x）=1+
sin2x，
（Ⅰ）设x=x0是函数y=f（x）图象的一条对称轴，求g（x0）的值；
（Ⅱ）求函数h（x）=f（x）+g（x）的单调递增区间。
），g（x）=1+sin2x，（Ⅰ）设x=x0是函数y=f（x）图象的一条对称轴，求g（x0）的值；
（Ⅱ）求函数h（x）=f（x）+g（x）的单调递增区间。
解：（Ⅰ）由题设知
，
因为x=x0是函数y=f（x）图象的一条对称轴，
所以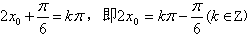
，
所以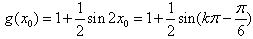
，
当k为偶数时，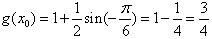
；
当k为奇数时，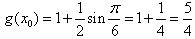
。
（Ⅱ）
当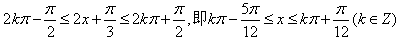
时，
函数
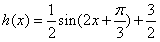是增函数，
故函数h（x）的单调递增区间是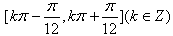
。
， 因为x=x0是函数y=f（x）图象的一条对称轴，
所以
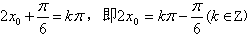，所以
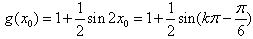，当k为偶数时，
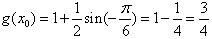； 当k为奇数时，
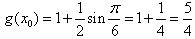。（Ⅱ）
当
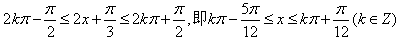时，函数
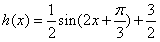是增函数，故函数h（x）的单调递增区间是
。 
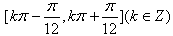练习册系列答案
相关题目
已知函数f（x）=
，则关于x的方程f2（x）+bf（x）+c=0有5个不同实数解的充要条件是（ ）
|
| A、b＜-2且c＞0 |
| B、b＞-2且c＜0 |
| C、b＜-2且c=0 |
| D、b≥-2且c=0 |
已知函数f（x）的图象如图所示，则函数的值域为（ ）