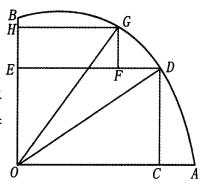
题目内容
【题目】平面直角坐标系xOy内,点![]() ,动点
,动点![]() 和Q关于原点O对称,
和Q关于原点O对称,![]() ,
,![]() .
.
(1)以原点O和点A为顶点作等腰直角三角形ABO,使![]() ,求向量
,求向量![]() 坐标;
坐标;
(2)若![]() 且P、M、A三点共线,求
且P、M、A三点共线,求![]() 的最小值;
的最小值;
(3)若![]() ,且
,且![]() ,
,![]() ,求直线AQ的解析式.
,求直线AQ的解析式.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)设出点B坐标,利用等腰直角三角形的两腰相等且两腰相互垂直,结合平面向量的坐标表示建立方程组求解即可;
(2)根据![]() 与
与![]() 共线,利用坐标运算列出方程得到
共线,利用坐标运算列出方程得到![]() ,利用模长公式表示
,利用模长公式表示![]() ,结合二次函数的性质即可求出最小值;
,结合二次函数的性质即可求出最小值;
(3)将![]() ,且
,且![]() ,
,![]() ,表示为坐标的形式,列出方程组,求出点Q的坐标,再求出对应的斜率,利用点斜式写出方程即可.
,表示为坐标的形式,列出方程组,求出点Q的坐标,再求出对应的斜率,利用点斜式写出方程即可.
(1)设![]() ,则
,则![]() ,
,![]()
由题意可得: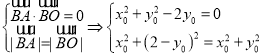
解得: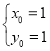 或
或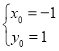
则向量![]() 坐标为
坐标为![]() 或
或![]()
(2)![]() ,
,![]()
因为![]() 与
与![]() 共线,所以
共线,所以![]()
得:![]()
![]()
当![]() 时,
时,![]() 取最小值
取最小值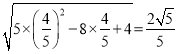
(3)因为![]() ,所以
,所以![]()
设![]() ,则
,则![]() ,
,![]() ,
,![]()
![]() ,
,![]()
因为![]() ,且
,且![]() ,
,![]()
所以![]() ,
,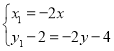 ,
,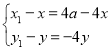
解得![]() 或
或![]()
即![]() 或
或![]()
当![]() 时,
时,![]() ,所以直线AQ的方程为
,所以直线AQ的方程为![]() ,即
,即![]()
当![]() 时,
时,![]() ,所以直线AQ的方程为
,所以直线AQ的方程为![]() ,即
,即![]()
综上所述,直线AQ的解析式为![]()

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目