Question

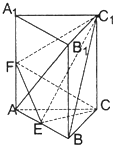（2009•红桥区二模）已知直棱柱ABC-A₁B₁C₁中，低面△ABC为等腰直角三角形，AC=BC=2

2

，∠ACB=90°，AA₁=4，E是AB的中点，F是AA₁的中点，
（Ⅰ）求证AB₁⊥平面CEF；
（Ⅱ）求异面直线AB₁与BC₁所成角的余弦值；
（Ⅲ）求三棱锥C₁-EFC的体积．

Answer 1

分析：（Ⅰ）由题意知，EF⊥AB₁，CE⊥AB₁，再由线面垂直的判断定理即可得到AB₁⊥平面CEF；也可用空间向量来处理；
（Ⅱ）由两直线的方向向量夹角的余弦值得到异面直线AB₁与BC₁所成角的余弦值；
（Ⅲ）要求三棱锥V的体积，即求三棱锥E-FCC₁的体积，而三棱锥E-FCC₁的高为E到AC的距离，△FCC₁的面积为

1

2

×2

2

×4=4

2

，则三棱锥体积可求．

解答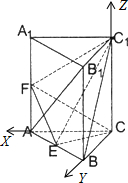：解：由于在直棱柱ABC-A₁B₁中，则CC₁⊥平面ABC，
又由∠ACB=90°，所以AC，CB，CC₁两两垂直
故可以C为原点，CA为x轴，CB为y轴，CC₁为Z轴，建立空间直角坐标系，
则A(2

2

，0，0)，B(0，2

2

，0)，C（0，0，0），B1(0，2

2

，4)，C₁（0，0，4）
故E(

2

，

2

，0)，F(2

2

，0，2)
（1）设平面CEF的法向量为

n

=(x，y，z)
由于

CE

=(

2

，

2

，0)，

CF

=(2

2

，0，2)
则

n • CE =0 n • CF =0

，即得

2 x+ 2 y=0 2 2 x+2z=0

故平面CEF的一个法向量为

n

=(1，-1，-

2

)
又由于

AB1

=(-2

2

，2

2

，4)=-2

2

(1，-1，-

2

)
故

AB1

∥

n

，所以AB₁⊥平面CEF；
（2）由（1）知，

AB1

=(-2

2

，2

2

，4)，

BC1

=(0，-2

2

，4)
则|

AB1

|=|(-2

2

，2

2

，4)|=4

2

，|

BC1

|=|(0，-2

2

，4)|=2

6

AB1

•

BC1

=(-2

2

，2

2

，4)•(0，-2

2

，4)=8
则cos＜

AB1

，

BC1

＞=

AB1 • BC1

| AB1 |•| BC1 |

=

8

4 2 •2 6

=

3

6

；
（3）由于三棱锥E-FCC₁的高为E到AC的距离，
△FCC₁的面积为

1

2

×2

2

×4=4

2

，
则三棱锥E-FCC₁的体积V=

1

3

×

1

2

BC×S△FCC1=

1

3

×

2

×

1

2

×2

2

×4=

8

3

又由VE-FCC1=VC1-EFC，则得三棱锥C₁-EFC的体积为

8

3

．

点评：本题考查直线与平面垂直的判定，线线角的求法以及空间几何体，考查空间想象能力、逻辑思维能力，是中档题．