题目内容

已知抛物线C：y=2x²与直线y=kx+2交于A，B两点，M是线段AB的中点，过M作x轴的垂线，垂足为N，若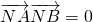 $数学公式$ ，则k=________．

$\text{[math]}$
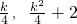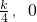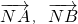分析：把y=kx+2代入y=2x²得2x²-kx-2=0由韦达定理得x₁+x₂= $\text{[math]}$ ，x₁•x₂=-1，求出M（ $\text{[math]}$ ），进一步得到N点的坐标为（ $\text{[math]}$ ）．表示出 $\text{[math]}$ ，利用向量的数量积根式求出 $\text{[math]}$ ，根据已知列出方程求出k的值．
解答：设A（x₁，2x₁²），B（x₂，2x₂²），
把y=kx+2代入y=2x²得2x²-kx-2=0
由韦达定理得x₁+x₂= $\text{[math]}$ ，x₁•x₂=-1，
所以M（ $\text{[math]}$ ），
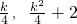所以N点的坐标为（ $\text{[math]}$ ）．
$\text{[math]}$ ， $\text{[math]}$ ，
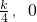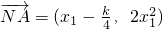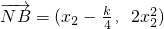所以 $\text{[math]}$ = $\text{[math]}$
= $\text{[math]}$
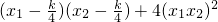
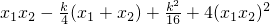
=-1 $\text{[math]}$
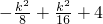
=3 $\text{[math]}$
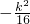
因为 $\text{[math]}$ ，
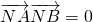所以3 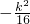$\text{[math]}$ =0
所以k= $\text{[math]}$
故答案为： $\text{[math]}$
点评：本题主要考查了直线与圆锥曲线的综合问题，解决的思路一般是将直线与圆锥曲线方程联立，利用韦达定理；考查了学生综合把握所学知识和基本的运算能力．

练习册系列答案

初中语文阅读卷系列答案

初中语文阅读试题方法详解系列答案

阅读写作e路通系列答案

初中语文阅读与写作系列答案

知识集锦名著导读系列答案

自能自测课时训练与示范卷系列答案

广东名著阅读全解全练系列答案

分级阅读与听力训练系列答案

新天地阶梯阅读系列答案

名校课堂系列答案

相关题目

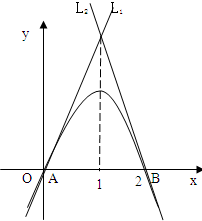已知抛物线C：y=-x²+2x，在点A（0，0），B（2，0）分别作抛物线的切线L₁、L₂．
（1）求切线L₁和L₂的方程；
（2）求抛物线C与切线L₁和L₂所围成的面积S．

已知抛物线C：y=x²+4x+

，过抛物线C上点M且与M处的切线垂直的直线称为抛物线C在点M的法线．
（1）若抛物线C在点M的法线的斜率为-

，求点M的坐标（x₀，y₀）；
（2）设P（-2，4）为C对称轴上的一点，在C上一定存在点，使得C在该点的法线通过点P．试求出这些点，以及C在这些点的法线方程．

已知抛物线C：y=x²，从原点O出发且斜率为k₀的直线l₀交抛物线C于一异于O点的点A₁（x₁，y₁），过A₁作一斜率为k₁的直线l₁交抛物线C于一异于A₁的点A₂（x₂，y₂）…，过A_n作斜率为k_n的直线l_n交抛物线C于一异于A_n的点A_n+1（x_n+1，y_n+1）且知k_n=k₀ⁿ⁺¹（k₀＞0且k₀≠1）．
（1）求x₁，x₂以及x_n与x_n+1之间的递推关系式；
（2）求{x_n}的通项公式．

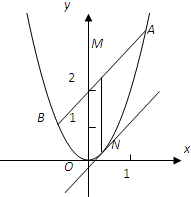已知抛物线C：y=2x²，直线y=kx+2交C于A，B两点，M是线段AB的中点，过M作轴的垂线交C于点N．
（1）求三角形OAB面积的最小值；
（2）证明：抛物线C在点N处的切线与AB平行；
（3）是否存在实数k使NANB，若存在，求k的值；若不存在，说明理由．

（2010•武汉模拟）已知抛物线C：y=

x2与直线l：y=kx-1没有公共点，设点P为直线l上的动点，过P作抛物线C的两条切线，A，B为切点．
（1）证明：直线AB恒过定点Q；
（2）若点P与（1）中的定点Q的连线交抛物线C于M，N两点，证明：