Question

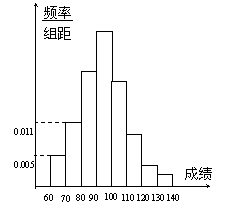
为了解某次测验成绩，在全年级随机地抽查了100名学生的成绩，得到频率分布直方图（如图），由于某种原因使部分数据丢失，但知道后5组的学生人数成等比数列，设90分以下人数为38，最大频率为b，则b的值为

0.32

．

Answer 1

分析：由已知中抽查了100名学生的成绩，90分以下人数为38，可得五组的累积频数为62，设第四组的频数为a，后5组的学生人数成等比数列的公比为q（0＜q＜1），结合最大频率为b，根据等比数列的前n项和公式及(

1

q

)4＜62，求出q，a，进而得到答案．

解答：解：由抽查了100名学生的成绩，90分以下人数为38，
则90分以上人数为100-38=62人，为后五组的累积频数
由于后5组的学生人数成等比数列，
设第四组的频数为a，公比为q（0＜q＜1），则
S₅=

a(1-q5)

1-q

=62=a（q⁴+q³+q²+q+1）
由各组人数均为整数，故(

1

q

)4＜62，
故q=

1

2

，a=32
则b=

a

100

=0.32
故答案为：0.32

点评：本题考查的知识点是频率分布直方图，本题难度较大，须要结合已知分析后5组的学生人数成等比数列的公比为q满足(

1

q

)4＜62（五组的累积频数）．