题目内容
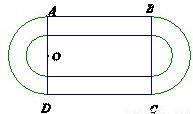
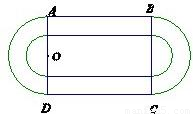
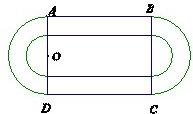 某学校要建造一个面积为10000平方米的运动场.如图,运动场是由一个矩形ABCD和分别以AD、BC为直径的两个半圆组成.跑道是一条宽8米的塑胶跑道,运动场除跑道外,其他地方均铺设草皮.已知塑胶跑道每平方米造价为150元,草皮每平方米造价为30元.
某学校要建造一个面积为10000平方米的运动场.如图,运动场是由一个矩形ABCD和分别以AD、BC为直径的两个半圆组成.跑道是一条宽8米的塑胶跑道,运动场除跑道外,其他地方均铺设草皮.已知塑胶跑道每平方米造价为150元,草皮每平方米造价为30元.(1)设半圆的半径OA=r(米),试建立塑胶跑道面积S与r的函数关系S(r);
(2)由于条件限制r∈[30,40],问当r取何值时,运动场造价最低?(精确到元)
分析:(1)跑道的面积等于一个大圆减去一个小圆加上一个大矩形减去一个小矩形,
(2)将实际问题的最值转化成数学问题的最值,用函数单调性求最值
(2)将实际问题的最值转化成数学问题的最值,用函数单调性求最值
解答:解:(1)塑胶跑道面积S=π[r2-(r-8)2]+8×
×2
=
+8πr-64π(8<r<
)
(2)设运动场造价为y则
y=150×(
+8πr-64π)+30×(10000-
-8πr+64π)
=300000+120(
+8πr)-7680π
∵r∈[30,40],函数y是r的减函数
∴当r=40,运动场造价最低为636510元
答:塑胶跑道面积S与r的函数关系S(r)=
+8πr-64π(8<r<
)
当r=40,运动场造价最低为636510元
| 10000-πr2 |
| 2r |
=
| 80000 |
| r |
| 100 | ||
|
(2)设运动场造价为y则
y=150×(
| 80000 |
| r |
| 80000 |
| r |
=300000+120(
| 80000 |
| r |
∵r∈[30,40],函数y是r的减函数
∴当r=40,运动场造价最低为636510元
答:塑胶跑道面积S与r的函数关系S(r)=
| 80000 |
| r |
| 100 | ||
|
当r=40,运动场造价最低为636510元
点评:本题考查建立数学模型的能力;用单调性求最值的方法.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
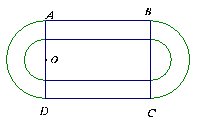 某学校要建造一个面积为10000平方米的运动场.如图,运动场是由一个矩形ABCD和分别以AD、BC为直径的两个半圆组成.跑道是一条宽8米的塑胶跑道,运动场除跑道外,其他地方均铺设草皮.已知塑胶跑道每平方米造价为150元,草皮每平方米造价为30元
某学校要建造一个面积为10000平方米的运动场.如图,运动场是由一个矩形ABCD和分别以AD、BC为直径的两个半圆组成.跑道是一条宽8米的塑胶跑道,运动场除跑道外,其他地方均铺设草皮.已知塑胶跑道每平方米造价为150元,草皮每平方米造价为30元