题目内容
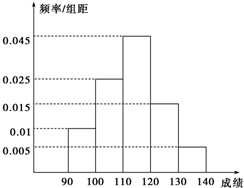 某校高二数学竞赛初赛考试后,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示,若130~140分数段的人数为2人.
某校高二数学竞赛初赛考试后,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示,若130~140分数段的人数为2人.(1)估计这所学校成绩在90~140分之间学生的参赛人数;
(2)估计参赛学生成绩的众数、中位数和平均数.
分析:(1)先求学校的总人数,再求90~140分之间的频率,总人数乘以此频率即为所求
(2)由频率分布直方图,结合求中位数和平均数的方法,即可找到众数,求得中位数和平均数
(2)由频率分布直方图,结合求中位数和平均数的方法,即可找到众数,求得中位数和平均数
解答:解:(1)∵130~140分数段的人数为2人
又130~140分数段的频率为:0.005×10=0.05
∴90~140分之间的人数为2÷0.05=40人
(2)90~100,100~110,110~120,120~130,130~140之间的人数依次为:
40×10×0.01=4人,40×10×0.025=10人,40×10×0.045=18人,40×10×0.015=6人,2人
∴参赛学生成绩的众数的估计值为115分
中位数的估计值为
+110=
≈113分
平均数的估计值为
=113分
又130~140分数段的频率为:0.005×10=0.05
∴90~140分之间的人数为2÷0.05=40人
(2)90~100,100~110,110~120,120~130,130~140之间的人数依次为:
40×10×0.01=4人,40×10×0.025=10人,40×10×0.045=18人,40×10×0.015=6人,2人
∴参赛学生成绩的众数的估计值为115分
中位数的估计值为
| 0.5-0.1-0.25 |
| 0.045 |
| 340 |
| 3 |
平均数的估计值为
| 95×4+105×10+115×18+125×6+135×2 |
| 40 |
点评:本题考查频率分布直方图和中位数平均数的求法,注意公式:频率=
的灵活应用
| 频数 |
| 样本容量 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 某校高二数学竞赛初赛考试后,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示,若130~140分数段的人数为2人.
某校高二数学竞赛初赛考试后,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示,若130~140分数段的人数为2人.

