题目内容
在下列命题中,
①“a=
”是“sina=1”的充要条件;
②(
+
)4的展开式中的常数项为2;
③设随机变量ξ~N(0,1),若P(ξ≥1)=p,则P(-1<ξ<0)=
-p;
④已知命题p:?x∈(0,+∞),3x>2x; 命题q:?x∈(-∞,0)3x>2x,则命题 p∧(¬q)为真命题;
其中所有正确命题的序号是( )
①“a=
| π |
| 2 |
②(
| x3 |
| 2 |
| 1 |
| x |
③设随机变量ξ~N(0,1),若P(ξ≥1)=p,则P(-1<ξ<0)=
| 1 |
| 2 |
④已知命题p:?x∈(0,+∞),3x>2x; 命题q:?x∈(-∞,0)3x>2x,则命题 p∧(¬q)为真命题;
其中所有正确命题的序号是( )
| A.①②④ | B.②③ | C.②③④ | D.①③④ |
①当sina=1时,α=
+2kπ,k∈Z,所以①错误.
②二项展开式的通项公式为Tk+1=
(
)4-k(
)k=
(
)4-kx12-4k,
由12-4k=0,得k=3,即常数项为T4=
×(
)=4×
=2,所以②正确.
③因为ξ~N(0,1),P(ξ≥1)=p,所以P(ξ≥1)=P(ξ≤-1)=p,
所以P(-1<ξ<0)=
=
=
-p.所以③正确.
④因为命题p为真,q为假,所以¬q为真,所以p∧(¬q)为真命题,所以④正确.
故选C.
| π |
| 2 |
②二项展开式的通项公式为Tk+1=
| C | k4 |
| x3 |
| 2 |
| 1 |
| x |
| C | k4 |
| 1 |
| 2 |
由12-4k=0,得k=3,即常数项为T4=
| C | 34 |
| 1 |
| 2 |
| 1 |
| 2 |
③因为ξ~N(0,1),P(ξ≥1)=p,所以P(ξ≥1)=P(ξ≤-1)=p,
所以P(-1<ξ<0)=
| 1-P(ξ≥1)-P(ξ≤-1) |
| 2 |
| 1-2p |
| 2 |
| 1 |
| 2 |
④因为命题p为真,q为假,所以¬q为真,所以p∧(¬q)为真命题,所以④正确.
故选C.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
 ”是“sina=1”的充要条件;
”是“sina=1”的充要条件; +
+ )4的展开式中的常数项为2;
)4的展开式中的常数项为2;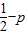 ;
;