题目内容
设f(x)=3-|x-1|,则∫-22f(x)dx=( )
分析:∫-22f(x)dx=∫-22(3-|x-1|)dx,将∫-22(3-|x-1|)dx转化成∫-21(2+x)dx+∫12(4-x)dx,然后根据定积分的定义先求出被积函数的原函数,然后求解即可.
解答:解:∫-22f(x)dx=∫-22(3-|x-1|)dx=∫-21(2+x)dx+∫12(4-x)dx=(2x+
x2)|-21+( 4x-
x2)|12=7
故选A.
| 1 |
| 2 |
| 1 |
| 2 |
故选A.
点评:本题主要考查了定积分,定积分运算是求导的逆运算,同时考查了转化与划归的思想,属于基础题.

练习册系列答案
相关题目
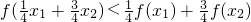 成立,则f(x)是定义在D上的β函数.
成立,则f(x)是定义在D上的β函数.