题目内容
已知f(x)是定义在正整数集N*上的函数,当x为奇数时f(x+1)-f(x)=1,当x为偶数时f(x+1)-f(x)=-3,且f(1)+f(2)=3.
(1)求证:f(1),f(3),f(5),…,f(2n-1)(n∈N*)成等差数列;
(2)求f(n)的解析式;
(3)求f(1)+f(2)+f(3)+f(4)+…+f(2 003)的值.
解析:
|
(1)由题意f(2m)-f(2m-1)=1,f(2m+1)-f(2m)=-3,相加得f(2m+1)-f(2m-1)=-2(m∈N*),则f(1),f(3),f(5),…,f(2m-1)(n∈N*)成等差数列,公差为-2. (2)同理,f(2m+2)-f(2m+1)=1,f(2m+1)-f(2m)=-3,相加得f(2m+2)-f(2m)=-2(m∈N*),则f(2),f(4),f(6),…,f(2m)(n∈N*)成等差数列,公差为-2.f(2)-f(1)=1,又f(1)+f(2)=3,所以f(1)=1,f(2)=2,当n为奇数时,n=2m-1,f(n)=f(2m-1)=f(1)+(m-1)(-2)=-n+2;当n为偶数时,n=2m,f(n)=f(2m)=f(2)+(m-1)(-2)=-n+4.所以f(n)= (3)f(1)+f(2)+f(3)+f(4)+…+f(2003)=[f(1)+f(3)+f(5)+f(7)+…+f(2003)]+[f(2)+f(4)+f(6)+f(8)+…+f(2002)]=1002×f(1)+ |
提示:
|
本题结构层层递进,(1)揭示数列{f(n)}每隔一项构成等差数列,从而可求出(2)中{f(n)}的通项公式,再求(3)中数列{f(n)}前2003项的和(转化为两个数列的和). |

 步步高达标卷系列答案
步步高达标卷系列答案 ) =
f(x)-f(y)
) =
f(x)-f(y) 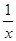 ) <2
) <2  ∪
∪ 上的奇函数,当
上的奇函数,当 时,f (x)的图象如图所示,那么f (x)的值域是
时,f (x)的图象如图所示,那么f (x)的值域是
