题目内容
某校高二(4)班组织学生报名参加国学社和摄影社,已知报名的每位学生至少报了一个社团,其中报名参加国学社的学生有2人,参加摄影社团的学生有5人,现从中选2人.设ξ为选出的学生中既报名参加国学社又报名参加摄影社的人数,且 .
.(Ⅰ)求高二(4)班报名参加社团的学生人数;
(Ⅱ)写出ξ的分布列并计算Eξ.
【答案】分析:(Ⅰ)利用对立事件的概率求出P(ξ=0),进而利用古典概型的概率计算公式即可得出答案;
(Ⅱ)利用古典概型的概率计算公式即可得出ξ的分布列,进而得出数学期望.
解答:解:(Ⅰ)设既报名参加国学社又报名参加摄影社的有x人,则该班报名总人数为(7-x)人.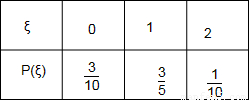
∵P(ξ>0)=P(ξ≥1)=1-P(ξ=0)=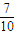 .
.
∴P(ξ=0)=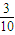 ,∴
,∴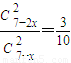 ,∴
,∴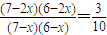 ,解得x=2.
,解得x=2.
故高二(4)班报名参加社团的学生有5人;
(Ⅱ)∵P(ξ=0)=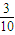 ,P(ξ=1)=
,P(ξ=1)=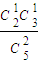 =
=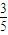 ,P(ξ=2)=
,P(ξ=2)=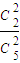 =
=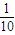 .
.
∴ξ的分布列为:
∴Eξ=0×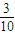
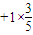
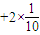 =
=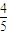 .
.
点评:熟练掌握对立事件的概率、古典概型的概率计算公式、离散型随机变量的概率分布和数学期望是解题的关键.
(Ⅱ)利用古典概型的概率计算公式即可得出ξ的分布列,进而得出数学期望.
解答:解:(Ⅰ)设既报名参加国学社又报名参加摄影社的有x人,则该班报名总人数为(7-x)人.

∵P(ξ>0)=P(ξ≥1)=1-P(ξ=0)=
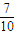 .
.∴P(ξ=0)=
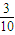 ,∴
,∴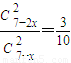 ,∴
,∴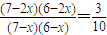 ,解得x=2.
,解得x=2.故高二(4)班报名参加社团的学生有5人;
(Ⅱ)∵P(ξ=0)=
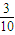 ,P(ξ=1)=
,P(ξ=1)=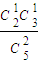 =
=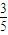 ,P(ξ=2)=
,P(ξ=2)=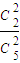 =
=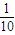 .
.∴ξ的分布列为:
∴Eξ=0×
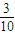
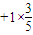
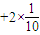 =
=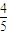 .
.点评:熟练掌握对立事件的概率、古典概型的概率计算公式、离散型随机变量的概率分布和数学期望是解题的关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 .
.