题目内容
已知函数y=f(x)是定义在(-∞,0)∪(0,+∞)上的奇函数,且当x>0时,f(x)=x2-2x-3,则当方程f(x)=k有三个不等实根时,k的取值范围是
- A.(-4,-3]∪[3,4)
- B.[-4,-3)∪(3,4]
- C.[-4,-3]∪[3,4]
- D.(-4,-3)∪(3,4)
D
分析:令x<0,则-x>0,由x>0时,f(x)=x2-2x-3,可求得f(-x),而f(x)为定义在R上的奇函数,从而可求得x<0时的解析式,再用分段函数表示函数f(x)的解析式画出图象,结合图象观察交点情况即可.
解答: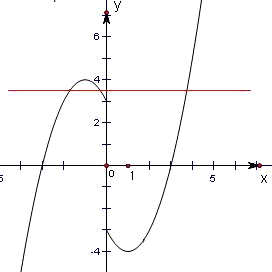 解:令x<0,则-x>0,
解:令x<0,则-x>0,
∵x>0时,f(x)=x2-2x-3,
∴f(-x)=(-x)2-2(-x)-3=x2+2x-3,
又f(x)为定义在R上的奇函数,
∴f(-x)=-f(x)=x2+2x-3,
∴f(x)=-x2-2x+3(x<0).
∴f(x)=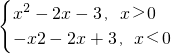 .其图象如图:
.其图象如图:
从图中可以得出,当方程f(x)=k有三个不等实根时,k的取值范围是(-4,-3)∪(3,4),
故选D.
点评:本题考查函数奇偶性的性质与函数的图象,求得x<0时的解析式是关键,考查运算与作图能力,属于基础题.
分析:令x<0,则-x>0,由x>0时,f(x)=x2-2x-3,可求得f(-x),而f(x)为定义在R上的奇函数,从而可求得x<0时的解析式,再用分段函数表示函数f(x)的解析式画出图象,结合图象观察交点情况即可.
解答:
 解:令x<0,则-x>0,
解:令x<0,则-x>0,∵x>0时,f(x)=x2-2x-3,
∴f(-x)=(-x)2-2(-x)-3=x2+2x-3,
又f(x)为定义在R上的奇函数,
∴f(-x)=-f(x)=x2+2x-3,
∴f(x)=-x2-2x+3(x<0).
∴f(x)=
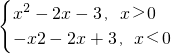 .其图象如图:
.其图象如图:从图中可以得出,当方程f(x)=k有三个不等实根时,k的取值范围是(-4,-3)∪(3,4),
故选D.
点评:本题考查函数奇偶性的性质与函数的图象,求得x<0时的解析式是关键,考查运算与作图能力,属于基础题.

练习册系列答案
相关题目
 已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为
已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为 已知函数y=f(x)的图象如图,则满足
已知函数y=f(x)的图象如图,则满足