题目内容
对于函数①f(x)=(x﹣2)2,②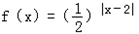 ,③f(x)=lg(|x﹣2|+1).
,③f(x)=lg(|x﹣2|+1).
有如下三个结论:
结论甲:f(x+2)是偶函数;
结论乙:f(x)在区间(﹣∞,2)上是减函数,在区间(2,+∞)上是增函数;
结论丙:f(x+2)﹣f(x)在(﹣∞,+∞)上是增函数.
能使甲、乙、丙三个结论均成立的所有函数的序号是( )。
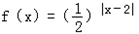 ,③f(x)=lg(|x﹣2|+1).
,③f(x)=lg(|x﹣2|+1).有如下三个结论:
结论甲:f(x+2)是偶函数;
结论乙:f(x)在区间(﹣∞,2)上是减函数,在区间(2,+∞)上是增函数;
结论丙:f(x+2)﹣f(x)在(﹣∞,+∞)上是增函数.
能使甲、乙、丙三个结论均成立的所有函数的序号是( )。
①

练习册系列答案
相关题目