Question

【题目】已知函数.

（1）若为的极值点，求实数的值；

（2）若在上为增函数，求实数的取值范围；

（2）若使方程有实根，求实数的取值范围.

Answer 1

【答案】（1） （2）（3）

【解析】试题分析：（1）求导若为的极值点，则从而求得结果．（2）由f（x）在[1，+∞）上为增函数，则有f′（x）≥0，x∈[1，+∞）上恒成立求解．若，则，∴在上为增函数成立，若，

对上恒成立. 对称轴为，从而在上为增函数. 只要即可（3）将a=-1代入，方程f(1x)(1x)3＝可转化为b=xlnx+x2-x3，x＞0上有解，只要求得函数g（x）=xlnx+x2-x3的值域即可．

试题解析：

（1）

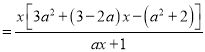
∵为的极值点，∴

∴且∴

又当时， ，从而为的极值点成立.

（2）因为在上为增函数，

所以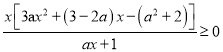在上恒成立.

若，则，∴在上为增函数成立

若，由对恒成立知.

所以对上恒成立.

令，其对称轴为，

因为，所以，从而在上为增函数.

所以只要即可，即

所以又因为

（3）若时，方程

可得

即在上有解

即求函数的值域.

令

由∵∴当时， ，

从而在上为增函数；当时， ，从而在上为减函数.

∴，而可以无穷小.∴的取值范围为.