题目内容
等轴双曲线C的中心在原点,焦点在x轴上,C与抛物线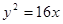 的准线交于A,B两点,
的准线交于A,B两点,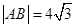 ,则C的实轴长为(
)
,则C的实轴长为(
)
A.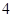 B.
B.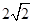 C.
C.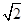 D.
D.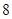
【答案】
A
【解析】
试题分析:设出双曲线方程,求出抛物线的准线方程,利用|AB|=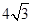 ,即可求得结论, 设等轴双曲线C的方程为x2-y2=λ.(1)∵抛物线y2=16x,2p=16,p=8,∴
,即可求得结论, 设等轴双曲线C的方程为x2-y2=λ.(1)∵抛物线y2=16x,2p=16,p=8,∴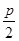 =4,∴抛物线的准线方程为x=-4,设等轴双曲线与抛物线的准线x=-4的两个交点A(-4,y),B(-4,-y)(y>0),则|AB|=|y-(-y)|=2y=
=4,∴抛物线的准线方程为x=-4,设等轴双曲线与抛物线的准线x=-4的两个交点A(-4,y),B(-4,-y)(y>0),则|AB|=|y-(-y)|=2y=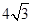 ,∴y=
,∴y=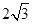 ,将x=-4,y=
,将x=-4,y=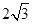 代入(1),得(-4)2-(
代入(1),得(-4)2-(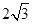 )2=λ,∴λ=4,∴等轴双曲线C的方程为x2-y2=4,即a=2,∴C的实轴长为4,选A.
)2=λ,∴λ=4,∴等轴双曲线C的方程为x2-y2=4,即a=2,∴C的实轴长为4,选A.
考点:双曲线和抛物线的简单性质.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目