题目内容
已知函数
（
（1）若函数
在
处有极值为
，求
的值；
（2）若对任意
，在
上单调递增，求的最小值．
（1）
则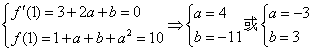
…………5分
当
时，
，所以函数有极值点；
当
，所以函数无极值点；
则的值为
．……………………………………7分
（2）解法一：
对任意的，都成立
则
对任意的，都成立
所以得
对任意的恒成立，
即
，又
，当
时
，得
所以 的最小值为
． …………15分
解法二：对任意的，都成立
即
对任意的，都成立,
即
.令
①当
；
②当
.
又∵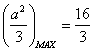
,∴
.
综上，的最小值为．
练习册系列答案
海淀课时新作业金榜卷系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
已知函数f(x)=
+
的定义域是（ ）
| 1-x2 |
| x2-1 |
| A、[-1，1] |
| B、{-1，1} |
| C、（-1，1） |
| D、（-∞，-1]∪[1，+∞） |