题目内容
设数列{an}满足a1=1,a2=2,an=(1)求数列{an}和{bn}的通项公式;
(2)记cn=nanbn(n=1,2,…),求数列{cn}的前n项和Sn.
解:(1)由an=![]() (an-1-an-2),
(an-1-an-2),
有an-an-1=![]() (an-1-an-2)(n=3,4…,).
(an-1-an-2)(n=3,4…,).
可得an-an-1=![]() (an-1-an-2)=
(an-1-an-2)=![]() [
[![]() (an-2-an-3)]
(an-2-an-3)]
=(![]() )2(an-2-an-3)
)2(an-2-an-3)
=……
=(![]() )n-2(a2-a1)=(
)n-2(a2-a1)=(![]() )n-2(n=3,4…,).
)n-2(n=3,4…,).
于是有an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
=(![]() )n-2+(
)n-2+(![]() )n-3+…+(
)n-3+…+(![]() )0+1
)0+1
=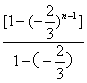 +1=
+1=![]() [8-3·(
[8-3·(![]() )n-1].
)n-1].
由题设b≠0,且对任意m∈Z+,有-1≤bm≤1![]() bm=1或bm=-1.
bm=1或bm=-1.
∵b1=1,由题设有-1≤b1+b2≤1![]() -2≤b2≤0,
-2≤b2≤0,
∴b2=-1.
同理,由题设有-1≤b2+b3≤1![]() 0≤b3≤2,
0≤b3≤2,
∴b3=1.
下面用反证法证明bn=(-1)n-1,
由题设可知|bn|=1,-1≤bm+…+bm=k≤1
假设{bn}存在相邻两项bm,bm=1的符号相同,
则有|bm+bm=1|=2|bm|=2,这与-1≤bm+…+bm=k≤1矛盾!
故{bn}的任意相邻两项bm,bm=1的符号都相反.
故bn=(-1)n-1
(2)若cn=nanbn,则cn=nanbn=![]() [8n(-1)n-1-3n(
[8n(-1)n-1-3n(![]() )n-1]
)n-1]
=![]() n(-1)n-1-
n(-1)n-1-![]() n(
n(![]() )n-1
)n-1
设dn=![]() n(-1)n-1=
n(-1)n-1=![]() nq1n-1,en=
nq1n-1,en=![]() n(
n(![]() )n-1=
)n-1=![]() nq2n-1.
nq2n-1.
对于数列{nqn-1}(q≠1),其前n项和Tn=1+2q+3q2+…+nqn-1,
Tn-qTn=1+q+…+qn-1-nqn=![]() -nqn
-nqn![]() Tn=
Tn=![]() (
(![]() -nqn).
-nqn).
所以{dn}前n项和为Dn=![]()
![]() [
[![]() -n(-1)n]
-n(-1)n]
=![]() [1-(2n+1)(-1)n],
[1-(2n+1)(-1)n],
{en}前n项和为En=![]()
![]() [
[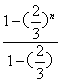 -n(
-n(![]() )n]
)n]
=![]() [3-(n+3)(
[3-(n+3)(![]() )n],
)n],
故{cn}前n项和为Sn=![]() [1-(2n+1)(-1)n]-
[1-(2n+1)(-1)n]-![]() [3-(n+3)(
[3-(n+3)(![]() )n]
)n]
=![]() [9(n+3)(
[9(n+3)(![]() )n+2(2n+1)(-1)n+1-25].
)n+2(2n+1)(-1)n+1-25].

 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案| π |
| 2 |
| 1 |
| 2an |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|