题目内容
已知α、β均为锐角,且 的值为
的值为
- A.-1
- B.1
- C.

- D.不存在
B
分析:由条件化简可得tanβ=tan( -α),再由α、β均为锐角,可得β=
-α),再由α、β均为锐角,可得β= -α,即α+β=
-α,即α+β= ,故可求tan(α+β)的值.
,故可求tan(α+β)的值.
解答:∵tanβ= =
= =tan(
=tan( -α),
-α),
又∵α、β均为锐角,∴β= -α,即α+β=
-α,即α+β= ,
,
∴tan(α+β)=tan =1,
=1,
故选B.
点评:本题考查同角三角函数的基本关系,两角和差的三角函数以及角的变换,体现了转化的数学思想,属于中档题.
分析:由条件化简可得tanβ=tan(
 -α),再由α、β均为锐角,可得β=
-α),再由α、β均为锐角,可得β= -α,即α+β=
-α,即α+β= ,故可求tan(α+β)的值.
,故可求tan(α+β)的值.解答:∵tanβ=
 =
= =tan(
=tan( -α),
-α),又∵α、β均为锐角,∴β=
 -α,即α+β=
-α,即α+β= ,
,∴tan(α+β)=tan
 =1,
=1,故选B.
点评:本题考查同角三角函数的基本关系,两角和差的三角函数以及角的变换,体现了转化的数学思想,属于中档题.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
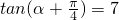 ,
, ,α,β均为锐角.
,α,β均为锐角.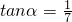 ,
,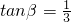 ,α,β均为锐角
,α,β均为锐角 如图,点B在以PA为直径的圆周上,点C在线段AB上,已知
如图,点B在以PA为直径的圆周上,点C在线段AB上,已知 如图,点B在以PA为直径的圆周上,点C在线段AB上,已知
如图,点B在以PA为直径的圆周上,点C在线段AB上,已知 ,设
,设 ,
, 均为锐角.
均为锐角. ;
; 的数量积
的数量积 的值.
的值.