题目内容
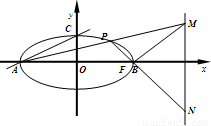
如图,设点P是椭圆 上的任意一点(异于左,右顶点A,B).
上的任意一点(异于左,右顶点A,B).(1)若椭圆E的右焦点为F,上顶点为C,求以F为圆心且与直线AC相切的圆的半径;
(2)设直线PA,PB分别交直线
 与点M,N,求证:PN⊥BM.
与点M,N,求证:PN⊥BM.
【答案】分析:(1)先求出直线AC的方程,由直线与圆心相切的性质可知,圆心到直线的距离等于半径可求r
(2)要证明PN⊥BM,只要证明 ,先设P的坐标,及直线AP,BP与直线x=
,先设P的坐标,及直线AP,BP与直线x= 的交点M,N,由A,P,M三点共线可知AM,BM的斜率相等,AN,BN的斜率相等,结合点P在椭圆上,可寻求P,M,N的坐标的关系,代入即可证明
的交点M,N,由A,P,M三点共线可知AM,BM的斜率相等,AN,BN的斜率相等,结合点P在椭圆上,可寻求P,M,N的坐标的关系,代入即可证明
解答:(1)解:由题意可知A(-2,0),B(2,0),C(0,1),F( ,0),
,0),
直线AC的方程为x-2y+2=0(2分)
设圆F的半径为r,则由以F为圆心的圆与直线AC相切可得圆心F到直线AC的距离为圆的半径r
∴r= =
= (5分)
(5分)
(2)设P(x,y),直线AP,BP分别交直线x= 于M(
于M( ),N(
),N( )两点
)两点
∵A,P,M三点共线
∴KAP=KAM即 ,整理可得,
,整理可得, (7分)
(7分)
同理可得, ,整理可得,
,整理可得, (9分)
(9分)
∴
∵P(x,y)在椭圆 上
上
∴ 即可得
即可得 (11分)
(11分)
∴ =
= ×
× =
= (13分)
(13分)
∴ =
= •
• =
=
= =
=
=
=
=0
∴PN⊥BM
点评:本题主要考查了点到直线的距离公司的应用,三点共线性质的应用,直线与圆的相交关系的应用,及向量的数量积的性质在证明几何关系中的应用,属于综合性试题
(2)要证明PN⊥BM,只要证明
 ,先设P的坐标,及直线AP,BP与直线x=
,先设P的坐标,及直线AP,BP与直线x= 的交点M,N,由A,P,M三点共线可知AM,BM的斜率相等,AN,BN的斜率相等,结合点P在椭圆上,可寻求P,M,N的坐标的关系,代入即可证明
的交点M,N,由A,P,M三点共线可知AM,BM的斜率相等,AN,BN的斜率相等,结合点P在椭圆上,可寻求P,M,N的坐标的关系,代入即可证明解答:(1)解:由题意可知A(-2,0),B(2,0),C(0,1),F(
 ,0),
,0),直线AC的方程为x-2y+2=0(2分)
设圆F的半径为r,则由以F为圆心的圆与直线AC相切可得圆心F到直线AC的距离为圆的半径r
∴r=
 =
= (5分)
(5分)(2)设P(x,y),直线AP,BP分别交直线x=
 于M(
于M( ),N(
),N( )两点
)两点∵A,P,M三点共线
∴KAP=KAM即
 ,整理可得,
,整理可得, (7分)
(7分)同理可得,
 ,整理可得,
,整理可得, (9分)
(9分)∴

∵P(x,y)在椭圆
 上
上∴
 即可得
即可得 (11分)
(11分)∴
 =
= ×
× =
= (13分)
(13分)∴
 =
= •
• =
=
=
 =
=
=

=

=0
∴PN⊥BM
点评:本题主要考查了点到直线的距离公司的应用,三点共线性质的应用,直线与圆的相交关系的应用,及向量的数量积的性质在证明几何关系中的应用,属于综合性试题

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
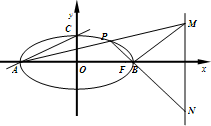 如图,设点P是椭圆
如图,设点P是椭圆 如图所示,F1、F2分别为椭圆C:
如图所示,F1、F2分别为椭圆C: (2012•深圳一模)如图,已知椭圆C:
(2012•深圳一模)如图,已知椭圆C: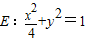 上的任意一点(异于左,右顶点A,B).
上的任意一点(异于左,右顶点A,B).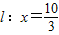 与点M,N,求证:PN⊥BM.
与点M,N,求证:PN⊥BM.